7.1.1 It’s All Audio Processing
We’ve entitled this chapter “Audio Processing” as if this is a separate topic within the realm of sound. But, actually, everything we do to audio is a form of processing. Every tool, plug-in, software application, and piece of gear is essentially an audio processor of some sort. What we set out to do in this chapter is to focus on particular kinds of audio processing, covering the basic concepts, applications, and underlying mathematics of these. For the sake of organization, we divide the chapter into processing related to frequency adjustments and processing related to amplitude adjustment, but in practice these two areas are interrelated.
7.1.2 Filters
You have seen in previous chapters how sounds are generally composed of multiple frequency components. Sometimes it’s desirable to increase the level of some frequencies or decrease others. To deal with frequencies, or bands of frequencies, selectively, we have to separate them out. This is done by means of filters. The frequency processing tools in the following sections are all implemented with one type of filter or another.
There are a number of ways to categorize filters. If we classify them according to what frequencies they attenuate, then we have these types of band filters:
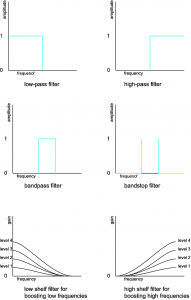
- low-pass filter – retains only frequencies below a given threshold
- high-pass filter – retains only frequencies above a given threshold
- bandpass filter – retains only frequencies within a given frequency band
- bandstop filter – eliminates frequencies within a given frequency band
- comb filter – attenuates frequencies in a manner that, when graphed in the frequency domain, has a “comb” shape. That is, multiples of some fundamental frequency are attenuated across the audible spectrum
- peaking filter – boosts or attenuates frequencies in a band
- shelving filters
- low-shelf filter – boosts or attenuates low frequencies
- high-shelf filter – boosts or attenuates high frequencies
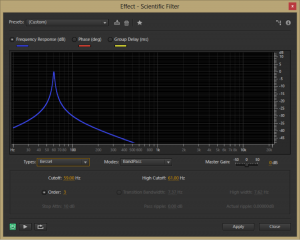
Filters that have a known mathematical basis for their frequency response graphs and whose behavior is therefore predictable at a finer level of detail are sometimes called scientific filters. This is the term Adobe Audition uses for Bessel, Butterworth, Chebyshev, and elliptical filters. The Bessel filter’s frequency response graph is shown in Figure 7.2
If we classify filters according to the way in which they are designed and implemented, then we have these types:
- IIR filters – infinite impulse response filters
- FIR filters – finite impulse response filters
Adobe Audition uses FIR filters for its graphic equalizer but IIR filters for its parametric equalizers (described below.) This is because FIR filters give more consistent phase response, while IIR filters give better control over the cutoff points between attenuated and non-attenuated frequencies. The mathematical and algorithmic differences of FIR and IIR filters are discussed in Section 3. The difference between designing and implementing filters in the time domain vs. the frequency domain is also explained in Section 3.
Convolution filters are a type of FIR filter that can apply reverberation effects so as to mimic an acoustical space. The way this is done is to record a short loud burst of sound in the chosen acoustical space and use the resulting sound samples as a filter on the sound to which you want to apply reverb. This is described in more detail in Section 7.1.6.
7.1.3 Equalization
Audio equalization, more commonly referred to as EQ, is the process of altering the frequency response of an audio signal. The purpose of equalization is to increase or decrease the amplitude of chosen frequency components in the signal. This is achieved by applying an audio filter.
EQ can be applied in a variety of situations and for a variety of reasons. Sometimes, the frequencies of the original audio signal may have been affected by the physical response of the microphones or loudspeakers, and the audio engineer wishes to adjust for these factors. Other times, the listener or audio engineer might want to boost the low end for a certain effect, “even out” the frequencies of the instruments, or adjust frequencies of a particular instrument to change its timbre, to name just a few of the many possible reasons for applying EQ.
Equalization can be achieved by either hardware or software. Two commonly-used types of equalization tools are graphic and parametric EQs. Within these EQ devices, low-pass, high-pass, bandpass, bandstop, low shelf, high shelf, and peak-notch filters can be applied.
7.1.4 Graphic EQ
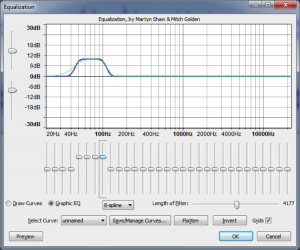
A graphic equalizer is one of the most basic types of EQ. It consists of a number of fixed, individual frequency bands spread out across the audible spectrum, with the ability to adjust the amplitudes of these bands up or down. To match our non-linear perception of sound, the center frequencies of the bands are spaced logarithmically. A graphic EQ is shown in Figure 7.3. This equalizer has 31 frequency bands, with center frequencies at 20 Hz, 25, Hz, 31 Hz, 40 Hz, 50 Hz, 63 Hz, 80 Hz, and so forth in a logarithmic progression up to 20 kHz. Each of these bands can be raised or lowered in amplitude individually to achieve an overall EQ shape.
While graphic equalizers are fairly simple to understand, they are not very efficient to use since they often require that you manipulate several controls to accomplish a single EQ effect. In an analog graphic EQ, each slider represents a separate filter circuit that also introduces noise and manipulates phase independently of the other filters. These problems have given graphic equalizers a reputation for being noisy and rather messy in their phase response. The interface for a graphic EQ can also be misleading because it gives the impression that you’re being more precise in your frequency processing than you actually are. That single slider for 1000 Hz can affect anywhere from one third of an octave to a full octave of frequencies around the center frequency itself, and consequently each actual filter overlaps neighboring ones in the range of frequencies it affects. In short, graphic EQs are generally not preferred by experienced professionals.
7.1.5 Parametric EQ
A parametric equalizer, as the name implies, has more parameters than the graphic equalizer, making it more flexible and useful for professional audio engineering. Figure 7.4 shows a parametric equalizer. The different icons on the filter column show the types of filters that can be applied. They are, from top to bottom, peak-notch (also called bell), low-pass, high-pass, low shelf, and high shelf filters. The available parameters vary according to the filter type. This particular filter is applying a low-pass filter on the fourth band and a high-pass filter on the fifth band.

[aside]The term “paragraphic EQ” is used for a combination of a graphic and parametric EQ, with sliders to change amplitudes and parameters that can be set for Q, cutoff frequency, etc.[/aside]
For the peak-notch filter, the frequency parameter corresponds to the center frequency of the band to which the filter is applied. For the low-pass, high-pass, low-shelf, and high-shelf filters, which don’t have an actual “center,” the frequency parameter represents the cut-off frequency. The numbered circles on the frequency response curve correspond to the filter bands. Figure 7.5 shows a low-pass filter in band 1 where the 6 dB down point – the point at which the frequencies are attenuated by 6 dB – is set to 500 Hz.
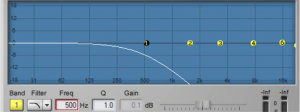
The gain parameter is the amount by which the corresponding frequency band is boosted or attenuated. The gain cannot be set for low or high-pass filters, as these types of filters are designed to eliminate all frequencies beyond or up to the cut-off frequency.
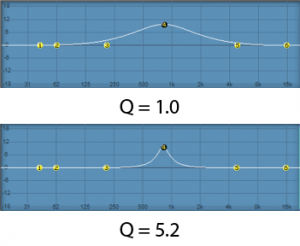
The Q parameter is a measure of the height vs. the width of the frequency response curve. A higher Q value creates a steeper peak in the frequency response curve compared to a lower one, as shown in Figure 7.6.
Some parametric equalizers use a bandwidth parameter instead of Q to control the range of frequencies for a filter. Bandwidth works inversely from Q in that a larger bandwidth represents a larger range of frequencies. The unit of measurement for bandwidth is typically an octave. A bandwidth value of 1 represents a full octave of frequencies between the 6 dB down points of the filter.
7.1.6 Reverb
cpu'[wpfilebase tag=file id=155 tpl=supplement /]
When you work with sound either live or recorded, the sound is generally captured with the microphone very close to the source of the sound. With the microphone very close, and particularly in an acoustically treated studio with very little reflected sound, it is often desired or even necessary to artificially add a reverberation effect to create a more natural sound, or perhaps to give the sound a special effect. Usually a very dry initial recording is preferred, so that artificial reverberation can be applied more uniformly and with greater control.
There are several methods for adding reverberation. Before the days of digital processing this was accomplished using a reverberation chamber. A reverberation chamber is simply a highly reflective, isolated room with very low background noise. A loudspeaker is placed at one end of the room and a microphone is placed at the other end. The sound is played into the loudspeaker and captured back through the microphone with all the natural reverberation added by the room. This signal is then mixed back into the source signal, making it sound more reverberant. Reverberation chambers vary in size and construction, some larger than others, but even the smallest ones would be too large for a home, much less a portable studio.
Because of the impracticality of reverberation chambers, most artificial reverberation is added to audio signals using digital hardware processors or software plug-ins, commonly called reverb processors. Software digital reverb processors use software algorithms to add an effect that sounds like natural reverberation. These are essentially delay algorithms that create copies of the audio signal that get spread out over time and with varying amplitudes and frequency responses.
A sound that is fed into a reverb processor comes out of that processor with thousands of copies or virtual reflections. As described in Chapter 4, there are three components of a natural reverberant field. A digital reverberation algorithm attempts to mimic these three components.
The first component of the reverberant field is the direct sound. This is the sound that arrives at the listener directly from the sound source without reflecting from any surface. In audio terms, this is known as the dry or unprocessed sound. The dry sound is simply the original, unprocessed signal passed through the reverb processor. The opposite of the dry sound is the wet or processed sound. Most reverb processors include a wet/dry mix that allows you to balance the direct and reverberant sound. Removing all of the dry signal leaves you with a very ambient effect, as if the actual sound source was not in the room at all.
The second component of the reverberant field is the early reflections. Early reflections are sounds that arrive at the listener after reflecting from the first one or two surfaces. The number of early reflections and their spacing vary as a function of the size and shape of the room. The early reflections are the most important factor contributing to the perception of room size. In a larger room, the early reflections take longer to hit a wall and travel to the listener. In a reverberation processor, this parameter is controlled by a pre-delay variable. The longer the pre-delay, the longer time you have between the direct sound and the reflected sound, giving the effect of a larger room. In addition to pre-delay, controls are sometimes available for determining the number of early reflections, their spacing, and their amplitude. The spacing of the early reflections indicates the location of the listener in the room. Early reflections that are spaced tightly together give the effect of a listener who is closer to a side or corner of the room. The amplitude of the early reflections suggests the distance from the wall. On the other hand, low amplitude reflections indicate that the listener is far away from the walls of the room.
The third component of the reverberant field is the reverberant sound. The reverberant sound is made of up all the remaining reflections that have bounced around many surfaces before arriving at the listener. These reflections are so numerous and close together that they are perceived as a continuous sound. Each time the sound reflects off a surface, some of the energy is absorbed. Consequently, the reflected sound is quieter than the sound that arrives at the surface before being reflected. Eventually all the energy is absorbed by the surfaces and the reverberation ceases. Reverberation time is the length of time it takes for the reverberant sound to decay by 60 dB, effectively a level so quiet it ceases to be heard. This is sometimes referred to as the RT60, or also the decay time. A longer decay time indicates a more reflective room.
Because most surfaces absorb high frequencies more efficiently than low frequencies, the frequency response of natural reverberation is typically weighted toward the low frequencies. In reverberation processors, there is usually a parameter for reverberation dampening. This applies a high shelf filter to the reverberant sound that reduces the level of the high frequencies. This dampening variable can suggest to the listener the type of reflective material on the surfaces of the room.
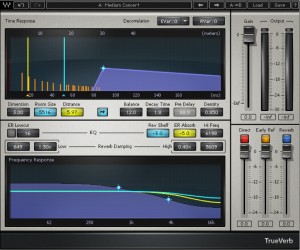
Figure 7.7 shows a popular reverberation plug-in. The three sliders at the bottom right of the window control the balance between the direct, early reflection, and reverberant sound. The other controls adjust the setting for each of these three components of the reverberant field.
The reverb processor pictured in Figure 7.8 is based on a complex computation of delays and filters that achieve the effects requested by its control settings. Reverbs such as these are often referred to as algorithmic reverbs, after their unique mathematical designs.
[aside]Convolution is a mathematical process that operates in the time-domain – which means that the input to the operation consists of the amplitudes of the audio signal as they change over time. Convolution in the time-domain has the same effect as mathematical filtering in the frequency domain, where the input consists of the magnitudes of frequency components over the frequency range of human hearing. Filtering can be done in either the time domain or the frequency domain, as will be explained in Section 3.[/aside]
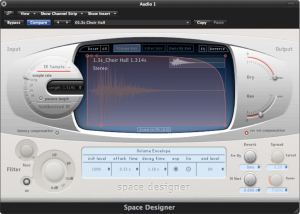
There is another type of reverb processor called a convolution reverb, which creates its effect using an entirely different process. A convolution reverb processor uses an impulse response (IR) captured from a real acoustic space, such as the one shown in Figure 7.8. An impulse response is essentially the recorded capture of a sudden burst of sound as it occurs in a particular acoustical space. If you were to listen to the IR, which in its raw form is simply an audio file, it would sound like a short “pop” with somewhat of a unique timbre and decay tail. The impulse response is applied to an audio signal by a process known as convolution, which is where this reverb effect gets its name. Applying convolution reverb as a filter is like passing the audio signal through a representation of the original room itself. This makes the audio sound as if it were propagating in the same acoustical space as the one in which the impulse response was originally captured, adding its reverberant characteristics.
With convolution reverb processors, you lose the extra control provided by the traditional pre-delay, early reflections, and RT60 parameters, but you often gain a much more natural reverberant effect. Convolution reverb processors are generally more CPU intensive than their more traditional counterparts, but with the speed of modern CPUs, this is not a big concern. Figure 7.8 shows an example of a convolution reverb plug-in.
7.1.7 Flange
Flange is the effect of combing out frequencies in a continuously changing frequency range. The flange effect is created by adding two identical audio signals, with one slightly delayed relative to the other, usually on the order of milliseconds. The effect involves continuous changes in the amount of delay, causing the combed frequencies to sweep back and forth through the audible spectrum.
In the days of analog equipment like tape decks, flange was created mechanically in the following manner: Two identical copies of an audio signal (usually music) were played, simultaneously and initially in sync, on two separate tape decks. A finger was pressed slightly against the edge (called the flange) of one of the tapes, slowing down its rpms. This delay in one of the copies of the identical waveforms being summed resulted in the combing out of a corresponding fundamental frequency and its harmonics. If the pressure increased continuously, the combed frequencies swept continuously through some range. When the finger was removed, the slowed tape would still be playing behind the other. However, pressing a finger against the other tape could sweep backward through the same range of combed frequencies and finally put the two tapes in sync again.
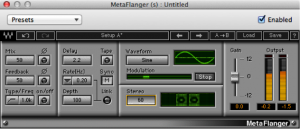
Artificial flange can be created through mathematical manipulation of the digital audio signal. However, to get a classic sounding flanger, you need to do more than simply delay a copy of the audio. This is because tape decks used in analog flanging had inherent variability that caused additional phase shifts and frequency combing, and thus they created a more complex sound. This fact hasn’t stopped clever software developers, however. The flange processor shown in Figure 7.9 from Waves is one that includes a tape emulation mode and includes presets that emulate several kinds of vintage tape decks and other analog equipment.
7.1.8 Vocoders
A vocoder (voice encoder) is a device that was originally developed for low bandwidth transmission of voice messages, but is now used for special voice effects in music production.
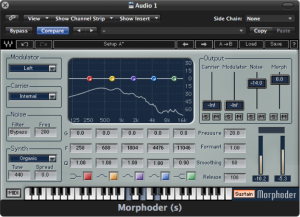
The original idea behind the vocoder was to encode the essence of the human voice by extracting just the most basic elements – the consonant sounds made by the vocal chords and the vowel sounds made by the modulating effect of the mouth. The consonants serve as the carrier signal and the vowels (also called formants) serve as the modulator signal. By focusing on the most important elements of speech necessary for understanding, the vocoder encoded speech efficiently, yielding a low bandwidth for transmission. The resulting voice heard at the other end of the transmission didn’t have the complex frequency components of a real human voice, but enough information was there for the words to be intelligible.
Today’s vocoders, used in popular music, combine voice and instruments to make the instrument sound as if it’s speaking, or conversely, to make a voice have a robotic or “techno” sound. The concept is still the same, however. Harmonically-rich instrumental music serves as the carrier, and a singer’s voice serves as the modulator. An example of a software vocoder plug-in is shown in Figure 7.10.
7.1.9 Autotuners
An autotuner is a software or hardware processor that is able to move a pitch of the human voice to the frequency of the nearest desired semitone. The original idea was that if the singer was slightly off-pitch, the autotuner could correct the pitch. For example, if the singer was supposed to be on the note A at a frequency of 440 Hz, and she was actually singing the note at 435 Hz, the autotuner would detect the discrepancy and make the correction.
[aside]Autotuners have also been used in popular music as an effect rather than a pitch correction. Snapping a pitch to set semitones can create a robotic or artificial sound that adds a new complexion to a song. Cher used this effect in her 1998 Believe album. In the 2000s, T-Pain further popularized its use in R&B and rap music.[/aside]
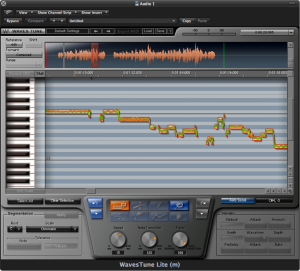
If you think about how an autotuner might be implemented, you’ll realize the complexities involved. Suppose you record a singer singing just the note A, which she holds for a few seconds. Even if she does this nearly perfectly, her voice contains not just the note A but harmonic overtones that are positive integer multiples of the fundamental frequency. Your algorithm for the software autotuner first must detect the fundamental frequency – call it $$f$$ – from among all the harmonics in the singer’s voice. It then must determine the actual semitone nearest to $$f$$. Finally, it has to move $$f$$ and all of its harmonics by the appropriate adjustment. All of this sounds possible when a single clear note is steady and sustained long enough for your algorithm to analyze it. But what if your algorithm has to deal with a constantly-changing audio signal, which is the nature of music? Also, consider the dynamic pitch modulation inherent in a singer’s vibrato, a commonly used vocal technique. Detecting individual notes, separating them one from the next, and snapping each sung note and all its harmonics to appropriate semitones is no trivial task. An example of an autotune processor is shown in Figure 7.11.
7.1.10 Dynamics Processing
7.1.10.1 Amplitude Adjustment and Normalization
One of the most straightforward types of audio processing is amplitude adjustment – something as simple as turning up or down a volume control. In the analog world, a change of volume is achieved by changing the voltage of the audio signal. In the digital world, it’s achieved by adding to or subtracting from the sample values in the audio stream – just simple arithmetic.
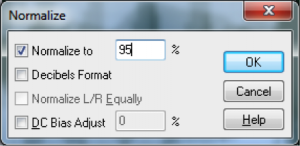
An important form of amplitude processing is normalization, which entails increasing the amplitude of the entire signal by a uniform proportion. Normalizers achieve this by allowing you to specify the maximum level you want for the signal, in percentages or dB, and increasing all of the samples’ amplitudes by an identical proportion such that the loudest existing sample is adjusted up or down to the desired level. This is helpful in maximizing the use of available bits in your audio signal, as well as matching amplitude levels across different sounds. Keep in mind that this will increase the level of everything in your audio signal, including the noise floor.
7.1.10.2 Dynamics Compression and Expansion
[wpfilebase tag=file id=141 tpl=supplement /]
Dynamics processing refers to any kind of processing that alters the dynamic range of an audio signal, whether by compressing or expanding it. As explained in Chapter 5, the dynamic range is a measurement of the perceived difference between the loudest and quietest parts of an audio signal. In the case of an audio signal digitized in n bits per sample, the maximum possible dynamic range is computed as the logarithm of the ratio between the loudest and the quietest measurable samples – that is, $$20\log_{10}\left ( \frac{2^{n-1}}{1/2} \right )dB$$. We saw in Chapter 5 that we can estimate the dynamic range as 6n dB. For example, the maximum possible dynamic range of a 16-bit audio signal is about 96 dB, while that of an 8-bit audio signal is about 48 dB.
The value of $$20\log_{10}\left ( \frac{2^{n-1}}{1/2} \right )dB$$ gives you an upper limit on the dynamic range of a digital audio signal, but a particular signal may not occupy that full range. You might have a signal that doesn’t have much difference between the loudest and quietest parts, like a conversation between two people speaking at about the same level. On the other hand, you might have at a recording of a Rachmaninoff symphony with a very wide dynamic range. Or you might be preparing a background sound ambience for a live production. In the final analysis, you may find that you want to alter the dynamic range to better fit the purposes of the recording or live performance. For example, if you want the sound to be less obtrusive, you may want to compress the dynamic range so that there isn’t such a jarring effect from a sudden difference between a quiet and a loud part.
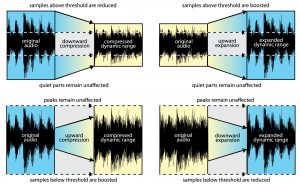
In dynamics processing, the two general possibilities are compression and expansion, each of which can be done in the upwards or downwards direction (Figure 7.13). Generally, compression attenuates the higher amplitudes and boosts the lower ones, the result of which is less difference in level between the loud and quiet parts, reducing the dynamic range. Expansion generally boosts the high amplitudes and attenuates the lower ones, resulting in an increase in dynamic range. To be precise:
- Downward compression attenuates signals that are above a given threshold, not changing signals below the threshold. This reduces the dynamic range.
- Upward compression boosts signals that are below a given threshold, not changing signals above the threshold. This reduces the dynamic range.
- Downward expansion attenuates signals that are below a given threshold, not changing signals above the threshold. This increases the dynamic range.
- Upward expansion boosts signals that are above a given threshold, not changing signals below the threshold. This increases the dynamic range.
The common parameters that can be set in dynamics processing are the threshold, attack time, and release time. The threshold is an amplitude limit on the input signal that triggers compression or expansion. (The same threshold triggers the deactivation of compression or expansion when it is passed in the other direction.) The attack time is the amount of time allotted for the total amplitude increase or reduction to be achieved after compression or expansion is triggered. The release time is the amount of time allotted for the dynamics processing to be “turned off,” reaching a level where a boost or attenuation is no longer being applied to the input signal.
Adobe Audition has a dynamics processor with a large amount of control. Most dynamics processor’s controls are simpler than this – allowing only compression, for example, with the threshold setting applying only to downward compression. Audition’s processor allows settings for compression and expansion and has a graphical view, and thus it’s a good one to illustrate all of the dynamics possibilities.
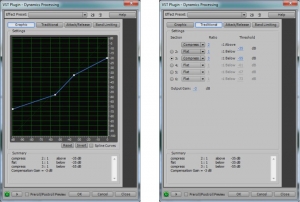
Figure 7.14 shows two views of Audition’s dynamics processor, the graphic and the traditional, with settings for downward and upward compression. The two views give the same information but in a different form.
In the graphic view, the unprocessed input signal is on the horizontal axis, and the processed input signal is on the vertical axis. The traditional view shows that anything above -35 dBFS should be compressed at a 2:1 ratio. This means that the level of the signal above -35 dBFS should be reduced by ½ . Notice that in the graphical view, the slope of the portion of the line above an input value of -35 dBFS is ½. This slope gives the same information as the 2:1 setting in the traditional view. On the other hand, the 3:1 ratio associated with the -55 dBFS threshold indicates that for any input signal below -55 dBFS, the difference between the signal and -55 dBFS should be reduced to 1/3 the original amount. When either threshold is passed (-35 or -55 dBFS), the attack time (given on a separate panel not shown) determines how long the compressor takes to achieve its target attenuation or boost. When the input signal moves back between the values of -35 dBFS and -55 dBFS, the release time determines how long it takes for the processor to stop applying the compression.
A simpler compressor – one of the ARDOUR LADSPA plug-ins, is shown in Figure 7.15. In addition to attack, release, threshold, and ratio controls, this compressor has knee radius and makeup gain settings. The knee radius allows you to shape the attack of the compression to something other than linear, giving a potentially smoother transition when it kicks in. The makeup gain setting (often called simply gain) allows you to boost the entire output signal after all other processing has been applied.

7.1.10.3 Limiting and Gating
[aside]A limiter could be thought of as a compressor with a compression ratio of infinity to 1. See the next section on dynamics compression.[/aside]
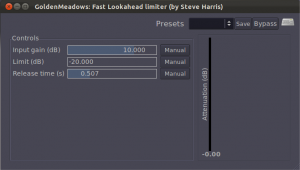
A limiter is a tool that prevents the amplitude of a signal from going over a given level. Limiters are often applied on the master bus, usually post-fader. Figure 7.16 shows the LADSPA Fast Lookahead Limiter plug-in. The input gain control allows you to increase the input signal before it is checked by the limiter. This limiter looks ahead in the input signal to determine if it is about to go above the limit, in which case the signal is attenuated by the amount necessary to bring it back within the limit. The lookahead allows the attenuation to happen almost instantly, and thus there is no attack time. The release time indicates how long it takes to go back to 0 attenuation when limiting the current signal amplitude is no longer necessary. You can watch this work in real-time by looking at the attenuation slider on the right, which bounces up and down as the limiting is put into effect.
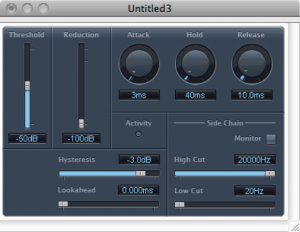
A gate allows an input signal to pass through only if it is above a certain threshold. A hard gate has only a threshold setting, typically a level in dB above or below which the effect is engaged. Other gates allow you to set an attack, hold, and release time to affect the opening, holding, and closing of the gate (Figure 7.18). Gates are sometimes used for drums or other instruments to make their attacks appear sharper and reduce the bleed from other instruments unintentionally captured in that audio signal.
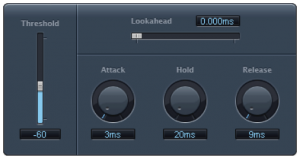
A noise gate is a specially designed gate that is intended to reduce the extraneous noise in a signal. If the noise floor is estimated to be, say, -80 dBFS, then a threshold can be set such that anything quieter than this level is blocked out, effectively transmitted as silence. A hysteresis control on a noise gate indicates that there is a threshold difference between opening and closing the gate. In the noise gate in Figure 7.18, the threshold of -50 dB and the hysteresis setting of -3 dB indicate that the gate closes at -50 dBFS and opens again at -47 dBFS. The side chain controls allow some signal other than the main input signal to determine when the input signal is gated. The side chain signal could cause the gate to close based on the amplitudes of only the high frequencies (high cut) or low frequencies (low cut).
In a practical sense, there is no real difference between a gate and a noise gate. A common misconception is that noise gates can be used to remove noise in a recording. In reality all they can really do is mute or reduce the level of the noise when only the noise is present. Once any part of the signal exceeds the gate threshold, the entire signal is allowed through the gate, including the noise. Still, it can be very effective at clearing up the audio in between words or phrases on a vocal track, or reducing the overall noise floor when you have multiple tracks with active regions but no real signal, perhaps during an instrumental solo.