6.2.3 Making and Loading Your Own Samples
[wpfilebase tag=file id=23 tpl=supplement /]
Sometimes you may find that you want a certain sound that isn’t available in your sampler. In that case, you may want to create your own sample
If you want to create a sampler patch that sounds like a real instrument, the first thing to do is find someone who has the instrument you’re interested in and get them to play different notes one at a time while you record them. To make sure you don’t have to stretch the pitch too far for any one sample, make sure you get a recording for at least three notes per octave within the instrument’s range.
[wpfilebase tag=file id=136 tpl=supplement /]
Keep in mind that the more samples you have, the more RAM space the sampler requires. If you have 500 MB worth of recorded samples and you want to use them all, the sampler is going to use up 500 MB of RAM on your computer. The trick is finding the right balance between having enough samples so that none of them get stretched unnaturally, but not so many that you use up all the RAM in your computer. As long as you have a real person and a real instrument to record, go ahead and get as many samples as you can. It’s much easier to delete the ones you don’t need than to schedule another recording session to get the two notes you forgot to record.Some instruments can sound different depending on how they are played. For example, a trumpet sounds very different with a mute inserted on the horn. If you want your sampler to be able to create the muted sound, you might be able to mimic it using filters in the sampler, but you’ll get better results by just recording the real trumpet with the mute inserted. Then you can program the sampler to play the muted samples instead of the unmuted ones when it receives a certain MIDI command.
Once you have all your samples recorded, you need to edit them and add all the metadata required by the sampler. In order for the sampler to do what it needs to do with the audio files, the files need to be in an uncompressed file format. Usually this is WAV or AIF format. Some samplers have a limit on the sampling rate they can work with. Make sure you convert the samples to the rate required by the sampler before you try to use them.
[wpfilebase tag=file id=137 tpl=supplement /]
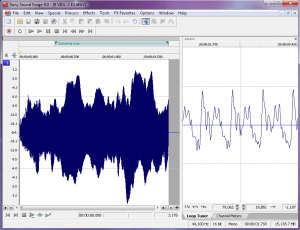
Figure 6.37 shows a loop defined in a sample editing program. On the left side of the screen you can see the overall waveform of the sample, in this case a violin. In the time ruler above the waveform you can see a green bar labeled Sustaining Loop. This is the portion of the sample that is looped. On the right side of the screen you can see a close up view of the loop point. The left half of the wave is the end of the sample, and the right part of the wave is the start of the loop point. The trick here is to line up the loop points so the two parts intersect with the zero amplitude cross point. This way you avoid any clicks or pops that might be introduced when the sampler starts looping the playback.The first bit of metadata you need to add to each sample is a loop start and loop end marker. Because you’re working with prerecorded sounds, the sound doesn’t necessarily keep playing just because you’re still holding the key down on the keyboard. You could just record your samples so they hold on for a long time, but that would use up an unnecessary amount of RAM. Instead, you can tell the sampler to play the file from the beginning and stop playing the file when the key on the keyboard is released. If the key is still down when the sampler reaches the end of the file, the sampler can start playing a small portion of the sample over and over in an endless loop until the note is released. The challenge here is finding a portion of the sample that loops naturally without any clicks or other swells in amplitude or harmonics.
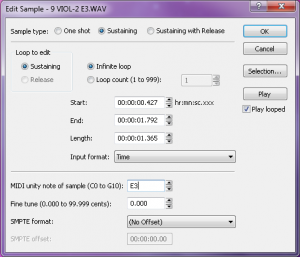
In some sample editors you can also add other metadata that saves you programming time later. For WAV and AIF files, you can add information about the root pitch of the sample and the range of notes this sample should cover. You can also add information about the loop behavior. For example, do you want the sample to continue to loop during the release of the amplitude envelope, or do you want it to start playing through to the end of the file? You could set the sample not to loop at all and instead play as a “one shot” sample. This means the sample ignores Note Off events and play the sample from beginning to end every time. Some samplers can read that metadata and do some pre-programming for you on the sampler when you load the sample.
Once the samples are ready, you can load them into the sampler. If you weren’t able to add the metadata about root key and loop type, you’ll have to add that manually into the sampler for each sample. You’ll also need to decide which notes trigger each sample and which velocities each sample responds to. This process of assigning root keys and key ranges to all your samples is a time consuming but essential process. Figure 6.39 shows a list of sample WAV files loaded in a software sampler. In the figure we have the sample “PianoC43.wav” selected. You can see in the center of the screen the span of keys that have been assigned to that sample. Along the bottom row of the screen you can see the root key, loop, and velocity assignments for that sample.
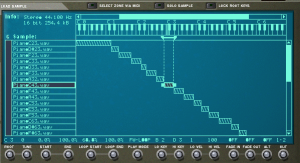
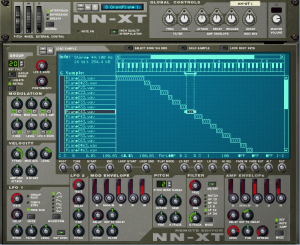
Once you have all your samples loaded and assigned, each sample can be passed through a filter and amplifier which can in turn be modulated using envelopes, LFO, and MIDI controller commands. Most samplers let you group samples together into zones or keygroups allowing you to apply a single set of filters, envelopes, etc. This feature can save a lot of time in programming. Imagine programming all of those settings on each of 100 samples without losing track of how far you are in the process. Figure 6.40 shows all the common synthesizer objects being applied to the “PianoC43.wav” sample.
6.3.2 Shaping Synthesizer Parameters with Envelopes and LFOs
Let’s make a sharp turn now from MIDI specifications to the mathematics and algorithms under the hood of synthesizers.
In Section 6.1.8.7, envelopes were discussed as a way of modifying the parameters of some synthesizer function – for example, the cutoff frequency of a low or high pass filter or the amplitude of a waveform. The mathematics of envelopes is easy to understand. The graph of the envelope shows time on the horizontal axis and a “multiplier” or coefficient on the vertical axis. The parameter is question is simply multiplied by the coefficient over time.
Envelopes can be generated by simple or complex functions. The envelope could be a simple sinusoidal, triangle, square, or sawtooth function that causes the parameter to go up and down in this regular pattern. In such cases, the envelope is called an oscillator. The term low-frequency oscillator (LFO) is used in synthesizers because the rate at which the parameter is caused to change is low compared to audible frequencies.
An ADSR envelope has a shape like the one shown in Figure 6.25. Such an envelope can be defined by the attack, decay, sustain, and release points, between which straight (or evenly curved) lines are drawn. Again, the values in the graph represent multipliers to be applied to a chosen parameter.
The exercise associated with this section invites you to modulate one or more of the parameters of an audio signal with an LFO and also with an ASDR envelope that you define yourself.
6.3.3 Type of Synthesis
6.3.3.1 Table-Lookup Oscillators and Wavetable Synthesis
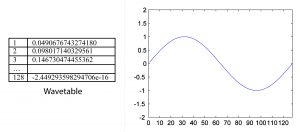
We have seen how single-frequency sound waves are easily generated by means of sinusoidal functions. In our example exercises, we’ve done this through computation, evaluating sine functions over time. In contrast, table-lookup oscillators generate waveforms by means of a set of look-up wavetables stored in contiguous memory locations. Each wavetable contains a list of sample values constituting one cycle of a sinusoidal wave, as illustrated in Figure 6.48. Multiple wavetables are stored so that waveforms of a wide range of frequencies can be generated.
[wpfilebase tag=file id=67 tpl=supplement /]
With a table-lookup oscillator, a waveform is created by advancing a pointer through a wavetable, reading the values, cycling back to the beginning of the table as necessary, and outputting the sound wave accordingly.
With a table of N samples representing one cycle of a waveform and an assumed sampling rate of r samples/s, you can generate a fundamental frequency of r/N Hz simply by reading the values out of the table at the sampling rate. This entails stepping through the indexes of the consecutive memory locations of the table. The wavetable in Figure 6.48 corresponds to a fundamental frequency of $$\frac{48000}{128}=375\: Hz$$.
Harmonics of the fundamental frequency of the wavetable can be created by skipping values or inserting extra values in between those in the table. For example, you can output a waveform with twice the frequency of the fundamental by reading out every other value in the table. You can output a waveform with ½ the frequency of the fundamental by reading each value twice, or by inserting values in between those in the table by interpolation.
The phase of the waveform can be varied by starting at an offset from the beginning of the wavetable. To start at a phase offset of $$p\pi $$ radians, you would start reading at index $$\frac{pN}{2}$$. For example, to start at an offset of π/2 in the wavetable of Figure 6.48, you would start at index $$\frac{\frac{1}{2}\ast 128}{2}=32$$.
To generate a waveform that is not a harmonic of the fundamental frequency, it’s necessary to add an increment to the consecutive indexes that are read out from the table. This increment i depends on the desired frequency f, the table length N, and the sampling rate r, defined by $$i=\frac{f\ast N}{r}$$. For example, to generate a waveform with frequency 750 Hz using the wavetable of Figure 6.48 and assuming a sampling rate of 48000 Hz, you would need an increment of $$i=\frac{750\ast 128}{48000}=2$$. We’ve chosen an example where the increment is an integer, which is good because the indexes into the table have to be integers.
What if you wanted a frequency of 390 Hz? Then the increment would be $$i=\frac{390\ast 128}{48000}=1.04$$, which is not an integer. In cases where the increment is not an integer, interpolation must be used. For example, if you want to go an increment of 1.04 from index 1, that would take you to index 2.04. Assuming that our wavetable is called table, you want a value equal to $$table\left [ 2 \right ]+0.04\ast \left ( table\left [ 3 \right ]-table\left [ 2 \right ] \right )$$. This is a rough way to do interpolation. Cubic spline interpolation can also be used as a better way of shaping the curve of the waveform. The exercise associated with this section suggests that you experiment with table-lookup oscillators in MATLAB.
[aside]The term “wavetable” is sometimes used to refer a memory bank of samples used by sound cards for MIDI sound generation. This can be misleading terminology, as wavetable synthesis is a different thing entirely.[/aside]
An extension of the use of table-lookup oscillators is wavetable synthesis. Wavetable synthesis was introduced in digital synthesizers in the 1970s by Wolfgang Palm in Germany. This was the era when the transition was being made from the analog to the digital realm. Wavetable synthesis uses multiple wavetables, combining them with additive synthesis and crossfading and shaping them with modulators, filters, and amplitude envelopes. The wavetables don’t necessarily have to represent simple sinusoidals but can be more complex waveforms. Wavetable synthesis was innovative in the 1970s in allowing for the creation of sounds not realizable with by solely analog means. This synthesis method has now evolved to the NWave-Waldorf synthesizer for the iPad.
6.3.3.2 Additive Synthesis
In Chapter 2, we introduced the concept of frequency components of complex waves. This is one of the most fundamental concepts in audio processing, dating back to the groundbreaking work of Jean-Baptiste Fourier in the early 1800s. Fourier was able to prove that any periodic waveform is composed of an infinite sum of single-frequency waveforms of varying frequencies and amplitudes. The single-frequency waveforms that are summed to make the more complex one are called the frequency components.
The implications of Fourier’s discovery are far reaching. It means that, theoretically, we can build whatever complex sounds we want just by adding sine waves. This is the basis of additive synthesis. We demonstrated how it worked in Chapter 2, illustrated by the production of square, sawtooth, and triangle waveforms. Additive synthesis of each of these waveforms begins with a sine wave of some fundamental frequency, f. As you recall, a square wave is constructed from an infinite sum of odd-numbered harmonics of f of diminishing amplitude, as in
$$!A\sin \left ( 2\pi ft \right )+\frac{A}{3}\sin \left ( 6\pi ft \right )+\frac{A}{5}\sin \left ( 10\pi ft \right )+\frac{A}{7}\sin \left ( 14\pi ft \right )+\frac{A}{9}\sin \left ( 18\pi ft \right )+\cdots$$
A sawtooth waveform can be constructed from an infinite sum of all harmonics of f of diminishing amplitude, as in
$$!\frac{2}{\pi }\left ( A\sin \left ( 2\pi ft \right )+\frac{A}{2}\sin \left ( 4\pi ft \right )+\frac{A}{3}\sin \left ( 6\pi ft \right )+\frac{A}{4}\sin \left ( 8\pi ft \right )+\frac{A}{5}\sin \left ( 10\pi ft \right )+\cdots \right )$$
A triangle waveform can be constructed from an infinite sum of odd-numbered harmonics of f that diminish in amplitude and vary in their sign, as in
$$!\frac{8}{\pi^{2} }\left ( A\sin \left ( 2\pi ft \right )+\frac{A}{3^{2}}\sin \left ( 6\pi ft \right )+\frac{A}{5^{2}}\sin \left ( 10\pi ft \right )-\frac{A}{7^{2}}\sin \left ( 14\pi ft \right )+\frac{A}{9^{2}}\sin \left ( 18\pi ft \right )-\frac{A}{11^{2}}\sin \left ( 22\pi ft \right )+\cdots \right )$$
These basic waveforms turn out to be very important in subtractive synthesis, as they serve as a starting point from which other more complex sounds can be created.
To be able to create a sound by additive synthesis, you need to know the frequency components to add together. It’s usually difficult to get the sound you want by adding waveforms from the ground up. In turns out that subtractive synthesis is often an easier way to proceed.
6.3.3.3 Subtractive Synthesis
The first synthesizers, including the Moog and Buchla’s Music Box, were analog synthesizers that made distinctive electronic sounds different from what is produced by traditional instruments. This was part of the fascination that listeners had for them. They did this by subtractive synthesis, a process that begins with a basic sound and then selectively removes frequency components. The first digital synthesizers imitated their analog precursors. Thus, when people speak of “analog synthesizers” today, they often mean digital subtractive synthesizers. The Subtractor Polyphonic Synthesizer shown in Figure 6.19 is an example of one of these.
The development of subtractive synthesis arose from an analysis of musical instruments and the way they create their sound, the human voice being among those instruments. Such sounds can be divided into two components: a source of excitation and a resonator. For a violin, the source is the bow being drawn across the string, and the resonator is the body of the violin. For the human voice, the source results from air movement and muscle contractions of the vocal chords, and the resonator is the mouth. In a subtractive synthesizer, the source could be a pulse, sawtooth, or triangle wave or random noise of different colors (colors corresponding to how the noise is spread out over the frequency spectrum). Frequently, preset patches are provided, which are basic waveforms with certain settings like amplitude envelopes already applied (another usage of the term patch). Filters are provided that allow you to remove selected frequency components. For example, you could start with a sawtooth wave and filter out some of the higher harmonic frequencies, creating something that sounds fairly similar to a stringed instrument. An amplitude envelope could be applied also to shape the attack, decay, sustain, and release of the sound.
The exercise suggests that you experiment with subtractive synthesis in C++ by beginning with a waveform, subtracting some of its frequency components, and applying an envelope.
6.3.3.4 Amplitude Modulation (AM)
Amplitude, phase, and frequency modulation are three types of modulation that can be applied to synthesize sounds in a digital synthesizer. We explain the mathematical operations below. In Section 0, we defined modulation as the process of changing the shape of a waveform over time. Modulation has long been used in analog telecommunication systems as a way to transmit a signal on a fixed frequency channel. The frequency on which a television or radio station is broadcast is referred to as the carrier signal and the message “written on” the carrier is called the modulator signal. The message can be encoded on the carrier signal in one of three ways: AM (amplitude modulation), PM (phase modulation), or FM (frequency modulation).
Amplitude modulation (AM) is commonly used in radio transmissions. It entails sending a message by modulating the amplitude of a carrier signal with a modulator signal.
In the realm of digital sound as created by synthesizers, AM can be used to generate a digital audio signal of N samples by application of the following equation:
[equation caption=”Equation 6.1 Amplitude modulation for digital synthesis”]
$$!a\left ( n \right )=\sin \left ( \omega _{c}n/r \right )\ast \left ( 1.0+A\cos\left ( \omega _{m}n/r \right ) \right )$$
for $$0\leq n\leq N-1$$
where N is the number of samples,
$$\omega _{c}$$ is the angular frequency of the carrier signal
$$\omega _{m}$$ is the angular frequency of the modulator signal
r is the sampling rate
and A is the amplitude
[/equation]
The process is expressed algorithmically in Algorithm 6.8. The algorithm shows that the AM synthesis equation must be applied to generate each of the samples for $$1\leq t\leq N$$.
[equation class=”algorithm” caption=”Algorithm 6.1 Amplitude modulation for digital synthesis”]
algorithm amplitude_modulation
/*
Input:
f_c, the frequency of the carrier signal
f_m, the frequency of a low frequency modulator signal
N, the number of samples you want to create
r, the sampling rate
A, to adjust the amplitude of the
Output:
y, an array of audio samples where the carrier has been amplitude modulated by the modulator */
{
for (n = 1 to N)
y[n] = sin(2*pi*f_c*n/r) * (1.0 + A*cos(2*pi*f_m*n/r));
}
[/equation]
Algorithm 6.1 can be executed at the MATLAB command line with the statements below, generating the graphs is Figure 6.49. Because MATLAB executes the statements as vector operations, a loop is not required. (Alternatively, a MATLAB program could be written using a loop.) For simplicity, we’ll assume $$A=1$$ in what follows.
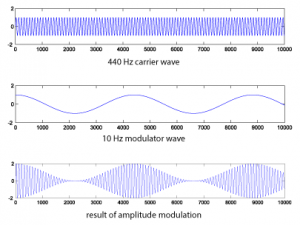
N = 44100; r = 44100; n = [1:N]; f_m = 10; f_c = 440; m = cos(2*pi*f_m*n/r); c = sin(2*pi*f_c*n/r); figure; AM = c.*(1.0 + m); plot(m(1:10000)); axis([0 10000 -2 2]); figure; plot(c(1:10000)); axis([0 10000 -2 2]); figure; plot(AM(1:10000)); axis([0 10000 -2 2]); sound(c, 44100); sound(m, 44100); sound(AM, 44100);
This yields the following graphs:
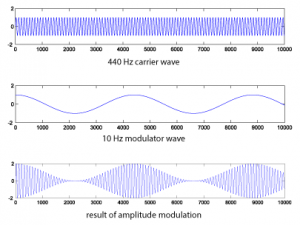
If you listen to the result, you’ll see that amplitude modulation creates a kind of tremolo effect.
The same process can be accomplished with more complex waveforms. HornsE04.wav is a 132,300-sample audio clip of horns playing, at a sampling rate of 44,100 Hz. Below, we shape it with a 440 Hz cosine wave (Figure 6.50).
N = 132300;
r = 44100;
c = audioread('HornsE04.wav');
n = [1:N];
m = sin(2*pi*10*n/r);
m = transpose(m);
AM2 = c .* (1.0 + m);
figure;
plot(c);
axis([0 132300 -2 2]);
figure;
plot(m);
axis([0 132300 -2 2]);
figure;
plot(AM2);
axis([0 132300 -2 2]);
sound(c, 44100);
sound(m, 44100);
sound(AM2, 44100);
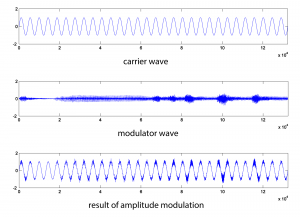
The audio effect is different, depending on which signal is chosen as the carrier and which as the modulator. Below, the carrier and modulator are reversed from the previous example, generating the graphs in Figure 6.51.
N = 132300;
r = 44100;
m = audioread('HornsE04.wav');
n = [1:N];
c = sin(2*pi*10*n/r);
c = transpose(c);
AM3 = c .* (1.0 + m);
figure;
plot(c);
axis([0 132300 -2 2]);
figure;
plot(m);
axis([0 132300 -2 2]);
figure;
plot(AM3);
axis([0 132300 -2 2]);
sound(c, 44100);
sound(m, 44100);
sound(AM3, 44100);
Amplitude modulation produces new frequency components in the resulting waveform at $$f_{c}+f_{m}$$ and $$f_{c}-f_{m}$$, where $$f_{c}$$ is the frequency of the carrier and $$f_{m}$$ is the frequency of the modulator. These are called sidebands. You can verify that the sidebands are at $$f_{c}+f_{m}$$ and $$f_{c}-f_{m}$$with a little math based on the properties of sines and cosines.
$$!\cos \left ( 2\pi f_{c}n \right )\left ( 1.0+\cos \left ( 2\pi f_{m}n \right ) \right )=\cos \left ( 2\pi f_{c}n \right )+\cos \left ( 2\pi f_{c}n \right )\cos \left ( 2\pi f_{m}n \right )=\cos \left ( 2\pi f_{c}n \right )+\frac{1}{2}\cos \left ( 2\pi \left ( f_{c}+f_{m} \right )n \right )+\frac{1}{2}\cos \left ( 2\pi \left ( f_{c}-f_{m} \right )n \right )$$
(The third step comes from the cosine product rule.) This derivation shows that there are three frequency components: one with frequency $$f_{c}$$, a second with frequency $$f_{c}+f_{m}$$, and a third with frequency $$f_{c}-f_{m}$$.
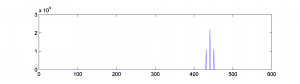
To verify this with an example, you can generate a graph of the sidebands in MATLAB by doing a Fourier transfer of the waveform generated by AM and plotting the magnitudes of the frequency components. MATLAB’s fft function does a Fourier transform of a vector of audio data, returning a vector of complex numbers. The abs function turns the complex numbers into a vector of magnitudes of frequency components. Then these values can be plotted with the plot function. We show the graph only from frequencies 1 through 600 Hz, since the only frequency components for this example lie in this range. Figure 6.52 shows the sidebands corresponding the AM performed in Figure 6.49. The sidebands are at 450 Hz and 460 Hz, as predicted.
figure; fftmag = abs(fft(AM)); plot(fftmag(1:600));
6.3.3.5 Ring Modulation
Ring modulation entails simply multiplying two signals. To create a digital signal using ring modulation, the Equation 6.2 can be applied.
[equation caption=”Equation 6.2 Ring modulation for digital synthesis”]
$$r\left ( n \right )=A_{1}\sin \left ( \omega _{1}n/r \right )\ast A_{2}\sin \left ( \omega _{2}n/r \right )$$
for $$0\leq n\leq N-1$$
where N is the number of samples,
r is the sampling rate,
where $$\omega _{1}$$ and $$\omega _{2}$$ are the angular frequencies of two signals, and $$A _{1}$$ and $$A _{2}$$ are their respective amplitudes
[/equation]
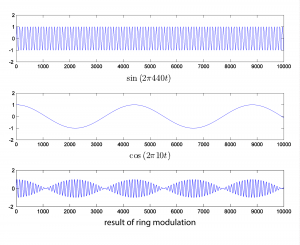
Since multiplication is commutative, there’s no sense in which one signal is the carrier and the other the modulator. Ring modulation is illustrated with two simple sine waves in Figure 6.53. The ring modulated waveform is generated with the MATLAB commands below. Again, we set amplitudes to 1.
N = 44100; r = 44100; n = [1:N]; w1 = 440; w2 = 10; rm = sin(2*pi*w1*n/r) .* cos(2*pi*w2*n/r); plot(rm(1:10000)); axis([1 10000 -2 2]);
6.3.3.6 Phase Modulation (PM)
Even more interesting audio effects can be created with phase (PM) and frequency modulation (FM). We’re all familiar with FM radio, which is based on sending a signal by frequency modulation. Phase modulation is not used extensively in radio transmissions because it can be ambiguous to interpret at the receiving end, but it turns out to be fairly easy to implement PM in digital synthesizers. Some hardware-based synthesizers that are commonly referred to as FM actually use PM synthesis internally – the Yamaha DX series, for example.
Recall that the general equation for a cosine waveform is $$A\cos \left ( 2\pi fn+\phi \right )$$ where f is the frequency and $$\phi$$ is the phase. Phase modulation involves changing the phase over time. Equation 6.3 uses phase modulation to generate a digital signal.
[equation caption=”Equation 6.3 Phase modulation for digital synthesis”]
$$p\left ( t \right )=A\cos \left ( \omega _{c}n/r+I\sin \left ( \omega _{m}n/r \right ) \right )$$
for $$0\leq n\leq N-1$$
where N is the number of samples,
$$\omega _{c}$$ is the angular frequency of the carrier signal,
$$\omega _{m}$$ is the angular frequency of the modulator signal,
r is the sampling rate
I is the index of modulation
and A is the amplitude
[/equation]
Phase modulation is demonstrated in MATLAB with the following statements:
N = 44100; r = 44100; n = [1:N]; f_m = 10; f_c = 440; w_m = 2 * pi * f_m; w_c = 2 * pi * f_c; A = 1; I = 1; p = A*cos(w_c * n/r + I*sin(w_m * n/r)); plot(p); axis([1 30000 -2 2]); sound(p, 44100);
The result is graphed in Figure 6.54.
Figure 6.54 Phase modulation using two sinusoidals, where $$\omega _{c}=2\pi 440$$ and $$\omega _{m}=2\pi 10$$
The frequency components shown in Figure 6.55 are plotted in MATLAB with
fp = fft2(p); figure; plot(abs(fp)); axis([400 480 0 18000]);
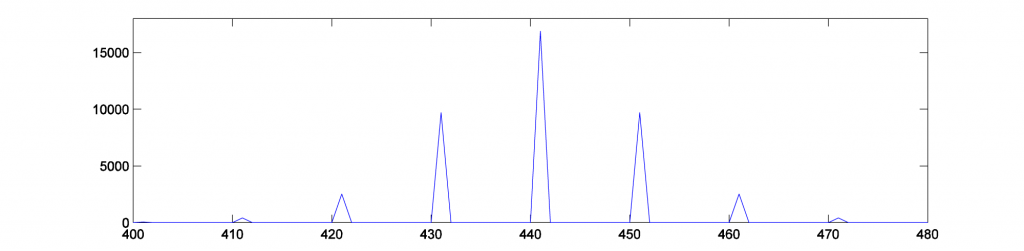
Phase modulation produces an infinite number of sidebands (many of whose amplitudes are too small to be detected). This fact is expressed in Equation 6.4.
[equation caption=”Equation 6.4 Phase modulation equivalence with additive synthesis”]
$$!\cos \left ( \omega _{c}n+I\sin \left ( \omega _{m}n \right ) \right )=\sum_{k=-\infty }^{\infty }J_{k}\left ( I \right )\cos \left ( \left [ \omega _{c}+k\omega _{m} \right ]n \right )$$
[/equation]
$$J_{k}\left ( I \right )$$ gives the amplitude of the frequency component for each kth component in the phase-modulated signal. These scaling functions $$J_{k}\left ( I \right )$$ are called Bessel functions of the first kind. It’s beyond the scope of the book to define these functions further. You can experiment for yourself to see that the frequency components have amplitudes that depend on I. If you listen to the sounds created, you’ll find that the timbres of the sounds can also be caused to change over time by changing I. The frequencies of the components, on the other hand, depend on the ratio of $$\omega _{c}/\omega _{m}$$. You can try varying the MATLAB commands above to experience the wide variety of sounds that can be created with phase modulation. You should also consider the possibilities of applying additive or subtractive synthesis to multiple phase-modulated waveforms.
The solution to the exercise associated with the next section gives a MATLAB .m program for phase modulation.
6.3.3.7 Frequency Modulation (FM)
We have seen in the previous section that phase modulation can be applied to the digital synthesis of a wide variety of waveforms. Frequency modulation is equally versatile and frequently used in digital synthesizers. Frequency modulation is defined recursively as follows:
[equation caption=”Equation 6.5 Frequency modulation for digital synthesis”]
$$f\left ( n \right )=A\cos \left ( p\left ( n \right ) \right )$$ and
$$p\left ( n \right )=p\left ( n-1 \right )+\frac{\omega _{c}}{r}+\left ( \frac{I\omega _{m}}{r}\ast \cos \left ( \frac{n\ast \omega _{m}}{r} \right ) \right )$$,
for $$1\leq n\leq N-1$$, and
$$p\left ( 0 \right )=\frac{\omega _{c}}{r}+ \frac{I\omega _{m}}{r}$$,
where N is the number of samples,
$$\omega_{c}$$ is the angular frequency of the carrier signal,
$$\omega_{m}$$ is the angular frequency of the modulator signal,
r is the sampling rate,
I is the index of modulation,
and A is amplitude
[/equation]
[wpfilebase tag=file id=69 tpl=supplement /]
Frequency modulation can yield results identical to phase modulation, depending on how inputs parameters are handled in the implementation. A difference between phase and frequency modulation is the perspective from which the modulation is handled. Obviously, the former is shaping a waveform by modulating the phase, while the latter is modulating the frequency. In frequency modulation, the change in the frequency can be handled by a parameter d, an absolute change in carrier signal frequency, which is defined by $$d=If_{m}$$. The input parameters $$N=44100$$, $$r=4100$$, $$f_{c}=880$$, $$f_{m}=10$$, $$A=1$$, and $$d=100$$ yield the graphs shown in Figure 6.56 and Figure 6.57. We suggest that you try to replicate these results by writing a MATLAB program based on Equation 6.5 defining frequency modulation.
Figure 6.56 Frequency modulation using two sinusoidals, where $$\omega _{c}=2\pi 880$$ and $$\omega _{m}=2\pi 10$$
6.4 References
In addition to references cited in previous chapters:
Boulanger, Richard, and Victor Lazzarini, eds. The Audio Programming Book. Cambridge, MA: The MIT Press, 2011.
Huntington, John. Control Systems for Live Entertainment. Boston: Focal Press, 1994.
Messick, Paul. Maximum MIDI: Music Applications in C++. Greenwich, CT: Manning Publications, 1998.
Schaeffer, Pierre. A la Recherche d’une Musique Concrète. Paris: Editions du Seuil, 1952.
7.1.1 It’s All Audio Processing
We’ve entitled this chapter “Audio Processing” as if this is a separate topic within the realm of sound. But, actually, everything we do to audio is a form of processing. Every tool, plug-in, software application, and piece of gear is essentially an audio processor of some sort. What we set out to do in this chapter is to focus on particular kinds of audio processing, covering the basic concepts, applications, and underlying mathematics of these. For the sake of organization, we divide the chapter into processing related to frequency adjustments and processing related to amplitude adjustment, but in practice these two areas are interrelated.
7.1.2 Filters
You have seen in previous chapters how sounds are generally composed of multiple frequency components. Sometimes it’s desirable to increase the level of some frequencies or decrease others. To deal with frequencies, or bands of frequencies, selectively, we have to separate them out. This is done by means of filters. The frequency processing tools in the following sections are all implemented with one type of filter or another.
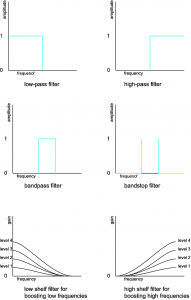
There are a number of ways to categorize filters. If we classify them according to what frequencies they attenuate, then we have these types of band filters:
- low-pass filter – retains only frequencies below a given threshold
- high-pass filter – retains only frequencies above a given threshold
- bandpass filter – retains only frequencies within a given frequency band
- bandstop filter – eliminates frequencies within a given frequency band
- comb filter – attenuates frequencies in a manner that, when graphed in the frequency domain, has a “comb” shape. That is, multiples of some fundamental frequency are attenuated across the audible spectrum
- peaking filter – boosts or attenuates frequencies in a band
- shelving filters
- low-shelf filter – boosts or attenuates low frequencies
- high-shelf filter – boosts or attenuates high frequencies
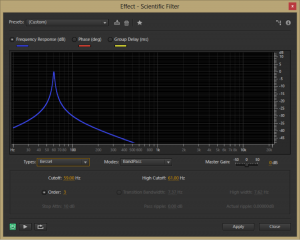
Filters that have a known mathematical basis for their frequency response graphs and whose behavior is therefore predictable at a finer level of detail are sometimes called scientific filters. This is the term Adobe Audition uses for Bessel, Butterworth, Chebyshev, and elliptical filters. The Bessel filter’s frequency response graph is shown in Figure 7.2
If we classify filters according to the way in which they are designed and implemented, then we have these types:
- IIR filters – infinite impulse response filters
- FIR filters – finite impulse response filters
Adobe Audition uses FIR filters for its graphic equalizer but IIR filters for its parametric equalizers (described below.) This is because FIR filters give more consistent phase response, while IIR filters give better control over the cutoff points between attenuated and non-attenuated frequencies. The mathematical and algorithmic differences of FIR and IIR filters are discussed in Section 3. The difference between designing and implementing filters in the time domain vs. the frequency domain is also explained in Section 3.
Convolution filters are a type of FIR filter that can apply reverberation effects so as to mimic an acoustical space. The way this is done is to record a short loud burst of sound in the chosen acoustical space and use the resulting sound samples as a filter on the sound to which you want to apply reverb. This is described in more detail in Section 7.1.6.
7.1.3 Equalization
Audio equalization, more commonly referred to as EQ, is the process of altering the frequency response of an audio signal. The purpose of equalization is to increase or decrease the amplitude of chosen frequency components in the signal. This is achieved by applying an audio filter.
EQ can be applied in a variety of situations and for a variety of reasons. Sometimes, the frequencies of the original audio signal may have been affected by the physical response of the microphones or loudspeakers, and the audio engineer wishes to adjust for these factors. Other times, the listener or audio engineer might want to boost the low end for a certain effect, “even out” the frequencies of the instruments, or adjust frequencies of a particular instrument to change its timbre, to name just a few of the many possible reasons for applying EQ.
Equalization can be achieved by either hardware or software. Two commonly-used types of equalization tools are graphic and parametric EQs. Within these EQ devices, low-pass, high-pass, bandpass, bandstop, low shelf, high shelf, and peak-notch filters can be applied.
7.1.4 Graphic EQ
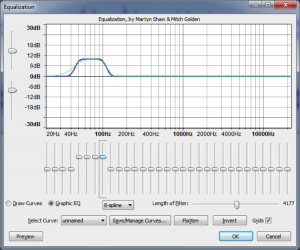
A graphic equalizer is one of the most basic types of EQ. It consists of a number of fixed, individual frequency bands spread out across the audible spectrum, with the ability to adjust the amplitudes of these bands up or down. To match our non-linear perception of sound, the center frequencies of the bands are spaced logarithmically. A graphic EQ is shown in Figure 7.3. This equalizer has 31 frequency bands, with center frequencies at 20 Hz, 25, Hz, 31 Hz, 40 Hz, 50 Hz, 63 Hz, 80 Hz, and so forth in a logarithmic progression up to 20 kHz. Each of these bands can be raised or lowered in amplitude individually to achieve an overall EQ shape.
While graphic equalizers are fairly simple to understand, they are not very efficient to use since they often require that you manipulate several controls to accomplish a single EQ effect. In an analog graphic EQ, each slider represents a separate filter circuit that also introduces noise and manipulates phase independently of the other filters. These problems have given graphic equalizers a reputation for being noisy and rather messy in their phase response. The interface for a graphic EQ can also be misleading because it gives the impression that you’re being more precise in your frequency processing than you actually are. That single slider for 1000 Hz can affect anywhere from one third of an octave to a full octave of frequencies around the center frequency itself, and consequently each actual filter overlaps neighboring ones in the range of frequencies it affects. In short, graphic EQs are generally not preferred by experienced professionals.
7.1.5 Parametric EQ
A parametric equalizer, as the name implies, has more parameters than the graphic equalizer, making it more flexible and useful for professional audio engineering. Figure 7.4 shows a parametric equalizer. The different icons on the filter column show the types of filters that can be applied. They are, from top to bottom, peak-notch (also called bell), low-pass, high-pass, low shelf, and high shelf filters. The available parameters vary according to the filter type. This particular filter is applying a low-pass filter on the fourth band and a high-pass filter on the fifth band.

[aside]The term “paragraphic EQ” is used for a combination of a graphic and parametric EQ, with sliders to change amplitudes and parameters that can be set for Q, cutoff frequency, etc.[/aside]
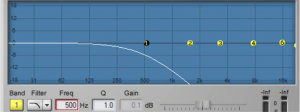
For the peak-notch filter, the frequency parameter corresponds to the center frequency of the band to which the filter is applied. For the low-pass, high-pass, low-shelf, and high-shelf filters, which don’t have an actual “center,” the frequency parameter represents the cut-off frequency. The numbered circles on the frequency response curve correspond to the filter bands. Figure 7.5 shows a low-pass filter in band 1 where the 6 dB down point – the point at which the frequencies are attenuated by 6 dB – is set to 500 Hz.
The gain parameter is the amount by which the corresponding frequency band is boosted or attenuated. The gain cannot be set for low or high-pass filters, as these types of filters are designed to eliminate all frequencies beyond or up to the cut-off frequency.
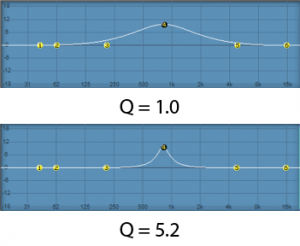
The Q parameter is a measure of the height vs. the width of the frequency response curve. A higher Q value creates a steeper peak in the frequency response curve compared to a lower one, as shown in Figure 7.6.
Some parametric equalizers use a bandwidth parameter instead of Q to control the range of frequencies for a filter. Bandwidth works inversely from Q in that a larger bandwidth represents a larger range of frequencies. The unit of measurement for bandwidth is typically an octave. A bandwidth value of 1 represents a full octave of frequencies between the 6 dB down points of the filter.
7.1.6 Reverb
cpu'[wpfilebase tag=file id=155 tpl=supplement /]
When you work with sound either live or recorded, the sound is generally captured with the microphone very close to the source of the sound. With the microphone very close, and particularly in an acoustically treated studio with very little reflected sound, it is often desired or even necessary to artificially add a reverberation effect to create a more natural sound, or perhaps to give the sound a special effect. Usually a very dry initial recording is preferred, so that artificial reverberation can be applied more uniformly and with greater control.
There are several methods for adding reverberation. Before the days of digital processing this was accomplished using a reverberation chamber. A reverberation chamber is simply a highly reflective, isolated room with very low background noise. A loudspeaker is placed at one end of the room and a microphone is placed at the other end. The sound is played into the loudspeaker and captured back through the microphone with all the natural reverberation added by the room. This signal is then mixed back into the source signal, making it sound more reverberant. Reverberation chambers vary in size and construction, some larger than others, but even the smallest ones would be too large for a home, much less a portable studio.
Because of the impracticality of reverberation chambers, most artificial reverberation is added to audio signals using digital hardware processors or software plug-ins, commonly called reverb processors. Software digital reverb processors use software algorithms to add an effect that sounds like natural reverberation. These are essentially delay algorithms that create copies of the audio signal that get spread out over time and with varying amplitudes and frequency responses.
A sound that is fed into a reverb processor comes out of that processor with thousands of copies or virtual reflections. As described in Chapter 4, there are three components of a natural reverberant field. A digital reverberation algorithm attempts to mimic these three components.
The first component of the reverberant field is the direct sound. This is the sound that arrives at the listener directly from the sound source without reflecting from any surface. In audio terms, this is known as the dry or unprocessed sound. The dry sound is simply the original, unprocessed signal passed through the reverb processor. The opposite of the dry sound is the wet or processed sound. Most reverb processors include a wet/dry mix that allows you to balance the direct and reverberant sound. Removing all of the dry signal leaves you with a very ambient effect, as if the actual sound source was not in the room at all.
The second component of the reverberant field is the early reflections. Early reflections are sounds that arrive at the listener after reflecting from the first one or two surfaces. The number of early reflections and their spacing vary as a function of the size and shape of the room. The early reflections are the most important factor contributing to the perception of room size. In a larger room, the early reflections take longer to hit a wall and travel to the listener. In a reverberation processor, this parameter is controlled by a pre-delay variable. The longer the pre-delay, the longer time you have between the direct sound and the reflected sound, giving the effect of a larger room. In addition to pre-delay, controls are sometimes available for determining the number of early reflections, their spacing, and their amplitude. The spacing of the early reflections indicates the location of the listener in the room. Early reflections that are spaced tightly together give the effect of a listener who is closer to a side or corner of the room. The amplitude of the early reflections suggests the distance from the wall. On the other hand, low amplitude reflections indicate that the listener is far away from the walls of the room.
The third component of the reverberant field is the reverberant sound. The reverberant sound is made of up all the remaining reflections that have bounced around many surfaces before arriving at the listener. These reflections are so numerous and close together that they are perceived as a continuous sound. Each time the sound reflects off a surface, some of the energy is absorbed. Consequently, the reflected sound is quieter than the sound that arrives at the surface before being reflected. Eventually all the energy is absorbed by the surfaces and the reverberation ceases. Reverberation time is the length of time it takes for the reverberant sound to decay by 60 dB, effectively a level so quiet it ceases to be heard. This is sometimes referred to as the RT60, or also the decay time. A longer decay time indicates a more reflective room.
Because most surfaces absorb high frequencies more efficiently than low frequencies, the frequency response of natural reverberation is typically weighted toward the low frequencies. In reverberation processors, there is usually a parameter for reverberation dampening. This applies a high shelf filter to the reverberant sound that reduces the level of the high frequencies. This dampening variable can suggest to the listener the type of reflective material on the surfaces of the room.
Figure 7.7 shows a popular reverberation plug-in. The three sliders at the bottom right of the window control the balance between the direct, early reflection, and reverberant sound. The other controls adjust the setting for each of these three components of the reverberant field.
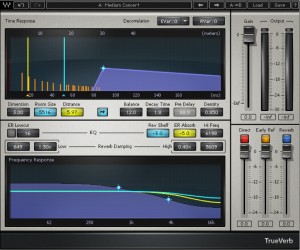
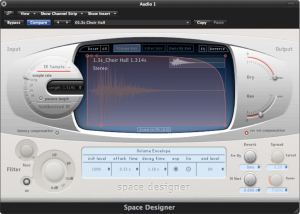
The reverb processor pictured in Figure 7.8 is based on a complex computation of delays and filters that achieve the effects requested by its control settings. Reverbs such as these are often referred to as algorithmic reverbs, after their unique mathematical designs.
[aside]Convolution is a mathematical process that operates in the time-domain – which means that the input to the operation consists of the amplitudes of the audio signal as they change over time. Convolution in the time-domain has the same effect as mathematical filtering in the frequency domain, where the input consists of the magnitudes of frequency components over the frequency range of human hearing. Filtering can be done in either the time domain or the frequency domain, as will be explained in Section 3.[/aside]
There is another type of reverb processor called a convolution reverb, which creates its effect using an entirely different process. A convolution reverb processor uses an impulse response (IR) captured from a real acoustic space, such as the one shown in Figure 7.8. An impulse response is essentially the recorded capture of a sudden burst of sound as it occurs in a particular acoustical space. If you were to listen to the IR, which in its raw form is simply an audio file, it would sound like a short “pop” with somewhat of a unique timbre and decay tail. The impulse response is applied to an audio signal by a process known as convolution, which is where this reverb effect gets its name. Applying convolution reverb as a filter is like passing the audio signal through a representation of the original room itself. This makes the audio sound as if it were propagating in the same acoustical space as the one in which the impulse response was originally captured, adding its reverberant characteristics.
With convolution reverb processors, you lose the extra control provided by the traditional pre-delay, early reflections, and RT60 parameters, but you often gain a much more natural reverberant effect. Convolution reverb processors are generally more CPU intensive than their more traditional counterparts, but with the speed of modern CPUs, this is not a big concern. Figure 7.8 shows an example of a convolution reverb plug-in.