In each chapter, we begin with basic concepts in Section 1 and give applications of those concepts in Section 2.  One main area where you can apply your understanding of sound waves is in the area of acoustics.  “Acoustics” is a large topic, and thus we have devoted a whole chapter to it.  Please refer to Chapter 4 for more on this topic.

Naturally occurring sound waves almost always contain more than one frequency. The frequencies combined into one sound are called the sound’s frequency components. A sound that has multiple frequency components is a complex sound wave. All the frequency components taken together constitute a sound’s frequency spectrum. This is analogous to the way light is composed of a spectrum of colors. The frequency components of a sound are experienced by the listener as multiple pitches combined into one sound.

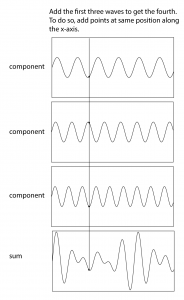
To understand frequency components of sound and how they might be manipulated, we can begin by synthesizing our own digital sound. Synthesis is a process of combining multiple elements to form something new. In sound synthesis, individual sound waves become one when their amplitude and frequency components interact and combine digitally, electrically, or acoustically. The most fundamental example of sound synthesis is when two sound waves travel through the same air space at the same time. Their amplitudes at each moment in time sum into a composite wave that contains the frequencies of both. Mathematically, this is a simple process of addition.

[wpfilebase tag=file id=29 tpl=supplement /]

We can experiment with sound synthesis and understand it better by creating three single-frequency sounds using an audio editing program like Audacity or Adobe Audition. Using the “Generate Tone” feature in Audition, we’ve created three separate sound waves – the first at 262 Hz (middle C on a piano keyboard), the second at 330 Hz (the note E), and the third at 393 Hz (the note G). They’re shown in Figure 2.14, each on a separate track. The three waves can be mixed down in the editing software – that is, combined into a single sound wave that has all three frequency components. The mixed down wave is shown on the bottom track.

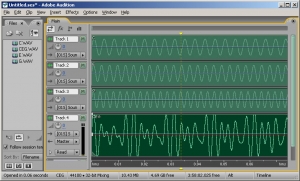
In a digital audio editing program like Audition, a sound wave is stored as a list of numbers, corresponding to the amplitude of the sound at each point in time. Thus, for the three audio tones generated, we have three lists of numbers. The mix-down procedure simply adds the corresponding values of the three waves at each point in time, as shown in Figure 2.15. Keep in mind that negative amplitudes (rarefactions) and positive amplitudes (compressions) can cancel each other out.

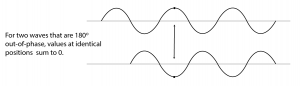
We’re able to hear multiple sounds simultaneously in our environment because sound waves can be added. Another interesting consequence of the addition of sound waves results from the fact that waves have phases. Consider two sound waves that have exactly the same frequency and amplitude, but the second wave arrives exactly one half cycle after the first – that is, 180^o out-of-phase, as shown in Figure 2.16. This could happen because the second sound wave is coming from a more distant loudspeaker than the first. The different arrival times result in phase-cancellations as the two waves are summed when they reach the listener’s ear. In this case, the amplitudes are exactly opposite each other, so they sum to 0.

We showed in the previous section how we can add frequency components to create a complex sound wave. The reverse of the sound synthesis process is sound analysis, which is the determination of the frequency components in a complex sound wave. In the 1800s, Joseph Fourier developed the mathematics that forms the basis of frequency analysis. He proved that any periodic sinusoidal function, regardless of its complexity, can be formulated as a sum of frequency components. These frequency components consist of a fundamental frequency and the harmonic frequencies related to this fundamental. Fourier’s theorem says that no matter how complex a sound is, it’s possible to break it down into its component frequencies – that is, to determine the different frequencies that are in that sound, and how much of each frequency component there is.

[aside]”Frequency response” has a number of related usages in the realm of sound.  It can refer to a graph showing the relative magnitudes of audible frequencies in a given sound.  With regard to an audio filter, the frequency response shows how a filter boosts or attenuates the frequencies in the sound to which it is applied.  With regard to loudspeakers, the frequency response is the way in which the loudspeakers boost or attenuate the audible frequencies.  With regard to a microphone, the frequency response is the microphone’s sensitivity to frequencies over the audible spectrum.[/aside]

Fourier analysis begins with the fundamental frequency of the sound – the frequency of the longest repeated pattern of the sound. Then all the remaining frequency components that can be yielded by Fourier analysis – i.e., the harmonic frequencies – are integer multiples of the fundamental frequency. By “integer multiple” we mean that if the fundamental frequency is $$f_0$$ , then each harmonic frequency $$f_n$$ is equal to for some non-negative integer $$(n+1)f_0$$.

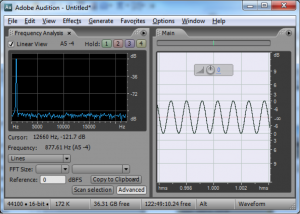
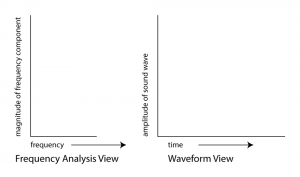
The Fourier transform is a mathematical operation used in digital filters and frequency analysis software to determine the frequency components of a sound. Figure 2.17 shows Adobe Audition’s waveform view and a frequency analysis view for a sound with frequency components at 262 Hz, 330 Hz, and 393 Hz. The frequency analysis view is to the left of the waveform view. The graph in the frequency analysis view is called a frequency response graph or simply a frequency response. The waveform view has time on the x-axis and amplitude on the y-axis. The frequency analysis view has frequency on the x-axis and the magnitude of the frequency component on the y-axis. (See Figure 2.18.) In the frequency analysis view in Figure 2.17, we zoomed in on the portion of the x-axis between about 100 and 500 Hz to show that there are three spikes there, at approximately the positions of the three frequency components. You might expect that there would be three perfect vertical lines at 262, 330, and 393 Hz, but this is because digitizing and transforming sound introduces some error. Still, the Fourier transform is accurate enough to be the basis for filters and special effects with sounds.

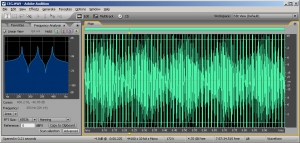
In the example just discussed, the frequencies that are combined in the composite sound never change. This is because of the way we constructed the sound, with three single-frequency waves that are held for one second. This sound, overall, is periodic because the pattern created from adding these three component frequencies is repeated over time, as you can see in the bottom of Figure 2.14.

Natural sounds, however, generally change in their frequency components as time passes. Consider something as simple as the word “information.”   When you say “information,” your voice produces numerous frequency components, and these change over time. Figure 2.19 shows a recording and frequency analysis of the spoken word “information.”

When you look at the frequency analysis view, don’t be confused into thinking that the x-axis is time. The frequencies being analyzed are those that are present in the sound around the point in time marked by the yellow line.

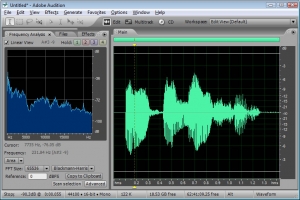
In music and other sounds, pitches – i.e., frequencies – change as time passes. Natural sounds are not periodic in the way that a one-chord sound is. The frequency components in the first second of such sounds are different from the frequency components in the next second. The upshot of this fact is that for complex non-periodic sounds, you have to analyze frequencies over a specified time period, called a window. When you ask your sound analysis software to provide a frequency analysis, you have to set the window size. The window size in Adobe Audition’s frequency analysis view is called “FFT size.” In the examples above, the window size is set to 65536, indicating that the analysis is done over a span of 65,536 audio samples. The meaning of this window size is explained in more detail in Chapter 7. What is important to know at this point is that there’s a tradeoff between choosing a large window and a small one. A larger window gives higher resolution across the frequency spectrum – breaking down the spectrum into smaller bands – but the disadvantage is that it “blurs” its analysis of the constantly changing frequencies across a larger span of time. A smaller window focuses on what the frequency components are in a more precise, short frame of time, but it doesn’t yield as many frequency bands in its analysis.

[wpfilebase tag=file id=108 tpl=supplement /]

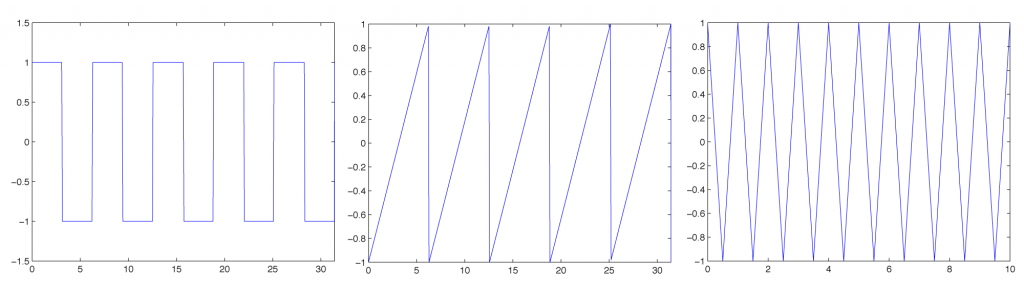
In Section 2.1.3, we categorized waves by the relationship between the direction of the medium’s movement and the direction of the wave’s propagation. Another useful way to categorize waves is by their shape – square, sawtooth, and triangle, for example. These waves are easily described in mathematical terms and can be constructed artificially by adding certain harmonic frequency components in the right proportions. You may encounter square, sawtooth, and triangle waves in your work with software synthesizers. Although these waves are non-sinusoidal – i.e., they don’t take the shape of a perfect sine wave – they still can be manipulated and played as sound waves, and they’re useful in simulating the sounds of musical instruments.

A square wave rises and falls regularly between two levels (Figure 2.20, left). A sawtooth wave rises and falls at an angle, like the teeth of a saw (Figure 2.20, center). A triangle wave rises and falls in a slope in the shape of a triangle (Figure 2.20, right). Square waves create a hollow sound that can be adapted to resemble wind instruments. Sawtooth waves can be the basis for the synthesis of violin sounds. A triangle wave sounds very similar to a perfect sine wave, but with more body and depth, making it suitable for simulating a flute or trumpet. The suitability of these waves to simulate particular instruments varies according to the ways in which they are modulated and combined.

[aside]If you add the even numbered frequencies, you still get a sawtooth wave, but with double the frequency compared to the sawtooth wave with all frequency components.[/aside]

[wpfilebase tag=file id=11 tpl=supplement /]

Non-sinusoidal waves can be generated by computer-based tools – for example, Reason or Logic, which have built-in synthesizers for simulating musical instruments. Mathematically, non-sinusoidal waveforms are constructed by adding or subtracting harmonic frequencies in various patterns. A perfect square wave, for example, is formed by adding all the odd-numbered harmonics of a given fundamental frequency, with the amplitudes of these harmonics diminishing as their frequencies increase. The odd-numbered harmonics are those with frequency  fn  where f is the fundamental frequency and n is a positive odd integer. A sawtooth wave is formed by adding all harmonic frequencies related to a fundamental, with the amplitude of each frequency component diminishing as the frequency increases. If you would like to look at the mathematics of non-sinusoidal waves more closely, see Section 2.3.2.

[separator top=”1″ bottom=”0″ style=”none”]

[aside]Although the term “impulse response” could technically be used for any instance of sound in the time domain, it is more often used to refer to instances of sound that are generated from a short burst of sound like a gun shot or balloon pop. In Chapter 7, you’ll see how an impulse response can be used to simulate the effect of an acoustical space on a sound.[/aside]

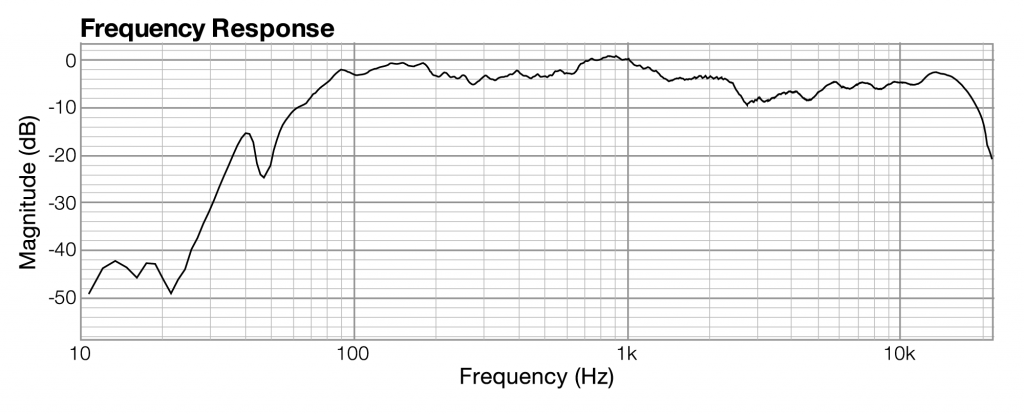
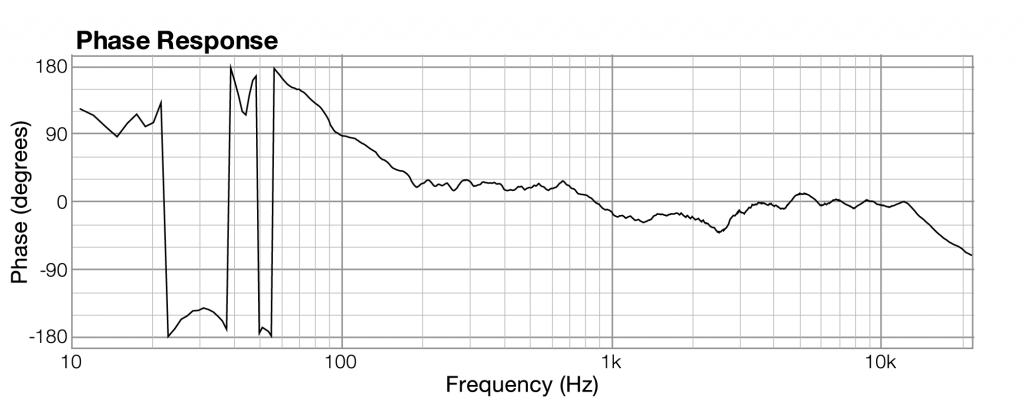
Section 2.2.3 introduces frequency response graphs, showing one taken from Adobe Audition. In fact, there are three interrelated graphs that are often used in sound analysis. Since these are used in this and later chapters, this is a good time to introduce you to these types of graphs. The three types of graphs are impulse response, frequency response, and phase response.

Impulse, frequency, and phase response graphs are simply different ways of storing and graphing the same set of data related to an instance of sound. Each type of graph represents the information in a different mathematical domain. The domains and ranges of the three types of sound graphs are given in Table 2.2.

 

[table caption=”Table 2.2 Domains and ranges of impulse, frequency, and phase response graphs” width=”80%”]

graph type,domain (x-axis),range (y-axis)

impulse response,time,amplitude of sound at each moment in time

frequency response,frequency,magnitude of frequency across the audible spectrum of sound

phase response,frequency,phase of frequency across the audible spectrum of sound

[/table]

Let’s look at an example of these three graphs, each associated with the same instance of sound. The graphs in the figures below were generated by sound analysis software called Fuzzmeasure Pro.

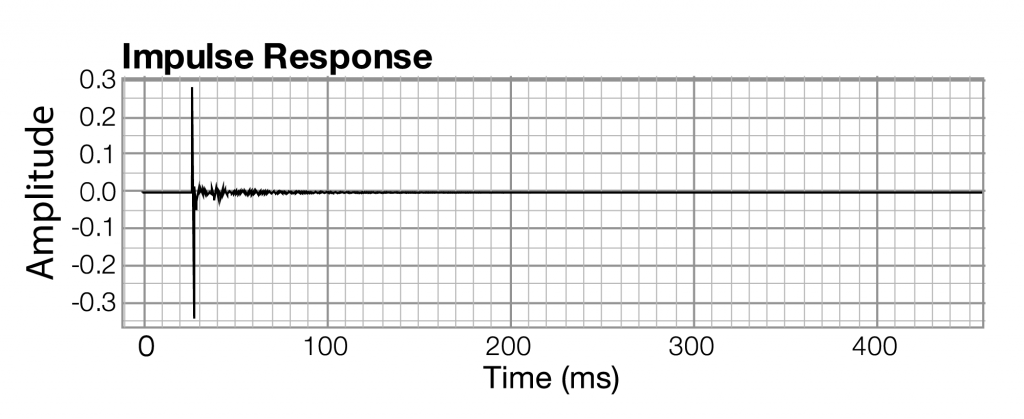
The impulse response graph shows the amplitude of the sound wave over time. The data used to draw this graph are produced by a microphone (and associated digitization hardware and software), which samples the amplitude of sound at evenly-spaced intervals of time. The details of this sound sampling process are discussed in Chapter 5. For now, all you need to understand is that when sound is captured and put into a form that can be handled by a computer, it is nothing more than a list of numbers, each number representing the amplitude of sound at a moment in time.

Related to each impulse response graph are two other graphs – a frequency response graph that shows “how much” of each frequency is present in the instance of sound, and a phase response graph that shows the phase that each frequency component is in. Each of these two graphs covers the audible spectrum. In Section 3, you’ll be introduced to the mathematical process – the Fourier transform – that converts sound data from the time domain to the frequency and phase domain.   Applying a Fourier transform to impulse response data – i.e., amplitude represented in the time domain – yields both frequency and phase information from which you can generate a frequency response graph and a phase response graph. The frequency response graph has the magnitude of the frequency on the y-axis on whatever scale is chosen for the graph. The phase response graph has phases ranging from -180° to 180° on the y-axis.

The main points to understand are these:

• A graph is a visualization of data.
• For any given instance of sound, you can analyze the data in terms of time, frequency, or phase, and you can graph the corresponding data.
• These different ways of representing sound – as amplitude of sound over time or as frequency and phase over the audible spectrum – contain essentially the same information.
• The Fourier transform can be used to transform the sound data from one domain of representation to another. The Fourier transform is the basis for processes applied at the user-level in sound measuring and editing software.
• When you work with sound, you look at it and edit it in whatever domain of representation is most appropriate for your purposes at the time. You’ll see this later in examples concerning frequency analysis of live performance spaces, room modes, precedence effect, and so forth.

It’s easy to model and manipulate sound waves in MATLAB, a mathematical modeling program. If you learn just a few of MATLAB’s built-in functions, you can create sine waves that represent sounds of different frequencies, add them, plot the graphs, and listen to the resulting sounds. Working with sound in MATLAB helps you to understand the mathematics involved in digital audio processing. In this section, we’ll introduce you to the basic functions that you can use for your work in digital sound. This will get you started with MATLAB, and you can explore further on your own. If you aren’t able to use MATLAB, which is a commercial product, you can try substituting the freeware program Octave. We introduce you briefly to Octave in Section 2.3.5. In future chapters, we’ll limit our examples to MATLAB because it is widely used and has an extensive Signal Processing Toolbox that is extremely useful in sound processing. We suggest Octave as a free alternative that can accomplish some, but not all, of the examples in remaining chapters.

Before we begin working with MATLAB, let’s review the basic sine functions used to represent sound. In the equation y = Asin(2πfx + θ), frequency f is assumed to be measured in Hertz. An equivalent form of the sine function, and one that is often used, is expressed in terms of angular frequency, ω, measured in units of radians/s rather than Hertz. Since there are 2π radians in a cycle, and Hz is cycles/s, the relationship between frequency in Hertz and angular frequency in radians/s is as follows:

[equation caption=”Equation2.7″]Let f be the frequency of a sine wave in Hertz. Then the angular frequency, ω, in radians/s, is given by

$$!\omega =2\pi f$$

 

[/equation]

We can now give an alternative form for the sine function.

[equation caption=”Equation 2.8″]A single-frequency sound wave with angular frequency ω, amplitude , and A phase θ is represented by the sine function

 

$$!y=A\sin \left ( \omega t+\theta \right )$$

[/equation]

In our examples below, we show the frequency in Hertz, but you should be aware of these two equivalent forms of the sine function.   MATLAB’s sine function expects angular frequency in Hertz, so f must be multiplied by 2π.

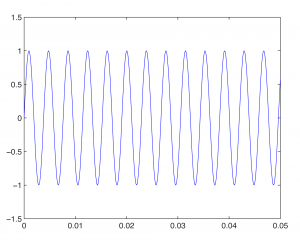
Now let’s look at how we can model sounds with sine functions in MATLAB. Middle C on a piano keyboard has a frequency of approximately 262 Hz. To create a sine wave in MATLAB at this frequency and plot the graph, we can use the fplot function as follows:

fplot('sin(262*2*pi*t)', [0, 0.05, -1.5, 1.5]);

The graph in Figure 2.30 pops open when you type in the above command and hit Enter. Notice that the function you want to graph is enclosed in single quotes. Also, notice that the constant π is represented as pi in MATLAB. The portion in square brackets indicates the limits of the horizontal and vertical axes. The horizontal axis goes from 0 to 0.05, and the vertical axis goes from –1.5 to 1.5.

If we want to change the amplitude of our sine wave, we can insert a value for A. If A > 1, we may have to alter the range of the vertical axis to accommodate the higher amplitude, as in

fplot('2*sin(262*2*pi*t)', [0, 0.05, -2.5, 2.5]);

After multiplying by A=2 in the statement above, the top of the sine wave goes to 2 rather than 1.

To change the phase of the sine wave, we add a value θ. Phase is essentially a relationship between two sine waves with the same frequency. When we add θ to the sine wave, we are creating a sine wave with a phase offset of θ compared to a sine wave with phase offset of 0. We can show this by graphing both sine waves on the same graph. To do so, we graph the first function with the command

fplot('2*sin(262*2*pi*t)', [0, 0.05, -2.5, 2.5]);

We then type

hold on

This will cause all future graphs to be drawn on the currently open figure. Thus, if we type

fplot('2*sin(262*2*pi*t+pi)', [0, 0.05, -2.5, 2.5]);

we have two phase-offset graphs on the same plot. In Figure 2.31, the 0-phase-offset sine wave is in red and the 180^o phase offset sine wave is in blue.

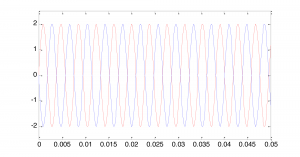
Notice that the offset is given in units of radians rather than degrees, 180^o being equal to radians.

To change the frequency, we change ω. For example, changing ω to 440*2*pi gives us a graph of the note A above middle C on a keyboard.

fplot('sin(440*2*pi*t)', [0, 0.05, -1.5, 1.5]);

The above command gives this graph:

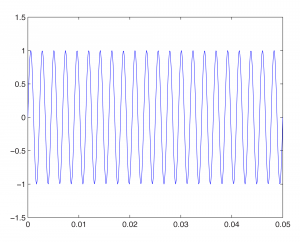
Then with

fplot('sin(262*2*pi*t)', [0, 0.05, -1.5, 1.5], 'red');

hold on

we get this figure:

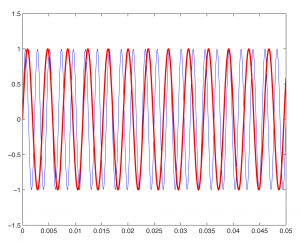
The 262 Hz sine wave in the graph is red to differentiate it from the blue 440 Hz wave.

The last parameter in the fplot function causes the graph to be plotted in red. Changing the color or line width also can be done by choosing Edit/Figure Properties on the figure, selecting the sine wave, and changing its properties.

We also can add sine waves to create more complex waves, as we did using Adobe Audition in Section 2.2.2. This is a simple matter of adding the functions and graphing the sum, as shown below.

figure

fplot('sin(262*2*pi*t)+sin(440*2*pi*t)', [0, 0.05, -2.5, 2.5]);

First, we type figure to open a new empty figure (so that our new graph is not overlaid on the currently open figure). We then graph the sum of the sine waves for the notes C and A. The result is this:

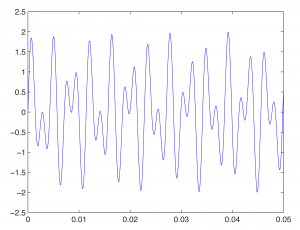
We’ve used the fplot function in these examples. This function makes it appear as if the graph of the sine function is continuous. Of course, MATLAB can’t really graph a continuous list of numbers, which would be infinite in length. The name MATLAB, in fact, is an abbreviation of “matrix laboratory.” MATLAB works with arrays and matrices. In Chapter 5, we’ll explain how sound is digitized such that a sound file is just an array of numbers. The plot function is the best one to use in MATLAB to graph these values. Here’s how this works.

First, you have to declare an array of values to use as input to a sine function. Let’s say that you want one second of digital audio at a sampling rate of 44,100 Hz (i.e., samples/s) (a standard sampling rate). Let’s set the values of variables for sampling rate sr and number of seconds s, just to remind you for future reference of the relationship between the two.

sr = 44100;
s = 1;

Now, to give yourself an array of time values across which you can evaluate the sine function, you do the following:

t = linspace(0,s, sr*s);

This creates an array of sr * s values evenly-spaced between and including the endpoints. Note that when you don’t put a semi-colon after a command, the result of the command is displayed on the screen. Thus, without a semi-colon above, you’d see the 44,100 values scroll in front of you.

To evaluate the sine function across these values, you type

y = sin(2*pi*262*t);

One statement in MATLAB can cause an operation to be done on every element of an array. In this example, y = sin(2*pi*262*t) takes the sine on each element of array t and stores the result in array y. To plot the sine wave, you type

plot(t,y);

Time is on the horizontal axis, between 0 and 1 second. Amplitude of the sound wave is on the vertical axis, scaled to values between -1 and 1. The graph is too dense for you to see the wave properly. There are three ways you can zoom in. One is by choosing Axes Properties from the graph’s Edit menu and then resetting the range of the horizontal axis. The second way is to type an axis command like the following:

axis([0 0.1 -2 2]);

This displays only the first 1/10 of a second on the horizontal axis, with a range of -2 to 2 on the vertical axis so you can see the shape of the wave better.

You can also ask for a plot of a subset of the points, as follows:

plot(t(1:1000),y(1:1000));

The above command plots only the first 1000 points from the sine function. Notice that the length of the two arrays must be the same for the plot function, and that numbers representing array indices must be positive integers. In general, if you have an array t of values and want to look at only the i^th to the j^th values, use t(i:j).

An advantage of generating an array of sample values from the sine function is that with that array, you actually can hear the sound. When you send the array to the wavplay or sound function, you can verify that you’ve generated one second’s worth of the frequency you wanted, middle C. You do this with

wavplay(y, sr);

(which works on Windows only) or, more generally,

sound(y, sr);

The first parameter is an array of sound samples. The second parameter is the sampling rate, which lets the system know how many samples to play per second.

MATLAB has other built-in functions for generating waves of special shapes. We’ll go back to using fplot for these. For example, we can generate square, sawtooth, and triangular waves with the three commands given below:

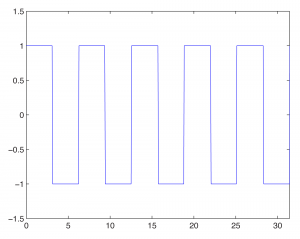
fplot('square(t)',[0,10*pi,-1.5,1.5]);

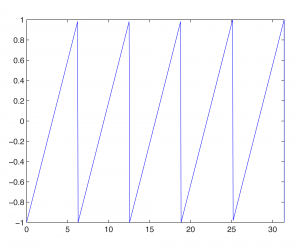
fplot('sawtooth(t)',[0,10*pi]);

fplot('2*pulstran(t,[0:10],''tripuls'')-1',[0,10]);

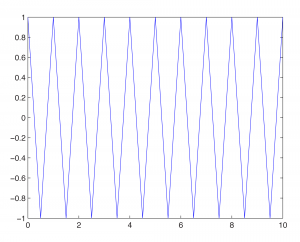
(Notice that the tripuls parameter is surrounded by two single quotes on each side.)

This section is intended only to introduce you to the basics of MATLAB for sound manipulation, and we leave it to you to investigate the above commands further. MATLAB has an extensive Help feature which gives you information on the built-in functions.

Each of the functions above can be created “from scratch” if you understand the nature of the non-sinusoidal waves. The ideal square wave is constructed from an infinite sum of odd-numbered harmonics of diminishing amplitude. More precisely, if f is the fundamental frequency of the non-sinusoidal wave to be created, then a square wave is constructed by the following infinite summation:

[equation caption=”Equation 2.9″]Let f be a fundamental frequency. Then a square wave created from this fundamental frequency is defined by the infinite summation

 

$$!\sum_{n=0}^{\infty }\frac{1}{\left ( 2n+1 \right )}\sin \left ( 2\pi \left ( 2n+1 \right )ft \right )$$

[/equation]

Of course, we can’t do an infinite summation in MATLAB, but we can observe how the graph of the function becomes increasingly square as we add more terms in the summation. To create the first four terms and plot the resulting sum, we can do

f1 = 'sin(2*pi*262*t) + sin(2*pi*262*3*t)/3 + sin(2*pi*262*5*t)/5 + sin(2*pi*262*7*t)/7';

fplot(f1, [0 0.01 -1 1]);

This gives the wave in Figure 2.38.

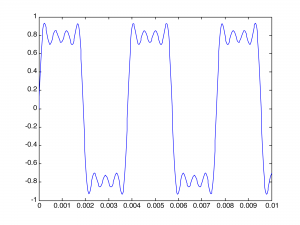
You can see that it is beginning to get square but has many ripples on the top. Adding four more terms gives further refinement to the square wave, as illustrated in Figure 2.39:

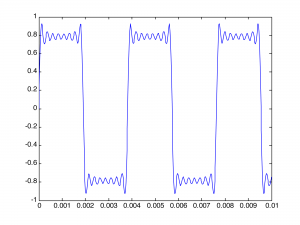
Creating the wave in this brute force manner is tedious. We can make it easier by using MATLAB’s sum function and its ability to do operations on entire arrays. For example, you can plot a 262 Hz square wave using 51 terms with the following MATLAB command:

fplot('sum(sin(2*pi*262*([1:2:101])*t)./([1:2:101]))',[0 0.005 -1 1])

The array notation [1:2:101] creates an array of 51 points spaced two units apart – in effect, including the odd harmonic frequencies in the summation and dividing by the odd number. The sum function adds up these frequency components. The function is graphed over the points 0 to 0.005 on the horizontal axis and –1 to 1 on the vertical axis. The ./ operation causes the division to be executed element by element across the two arrays.

The sawtooth wave is an infinite sum of all harmonic frequencies with diminishing amplitudes, as in the following equation:

[equation caption”Equation 2.10″]Let f be a fundamental frequency. Then a sawtooth wave created from this fundamental frequency is defined by the infinite summation

 

$$!\frac{2}{\pi }\sum_{n=1}^{\infty }\frac{\sin \left ( 2\pi n\, ft \right )}{n}$$

[/equation]

2/π is a scaling factor to ensure that the result of the summation is in the range of -1 to 1.

The sawtooth wave can be plotted by the following MATLAB command:

fplot('-sum((sin(2*pi*262*([1:100])*t)./([1:100])))',[0 0.005 -2 2])

The triangle wave is an infinite sum of odd-numbered harmonics that alternate in their signs, as follows:

[equation caption=”Equation 2.11″]Let f be a fundamental frequency. Then a triangle wave created from this fundamental frequency is defined by the infinite summation

 

$$!\frac{8}{\pi ^{2}}\sum_{n=0}^{\infty }\left ( \frac{sin\left ( 2\pi \left ( 4n+1 \right )ft \right )}{\left ( 4n+1 \right )^{2}} \right )-\left ( \frac{\sin \left ( 2\pi \left ( 4n+3 \right )ft \right )}{\left ( 4n+3 \right )^{2}} \right )$$

[/equation]

8/π^2 is a scaling factor to ensure that the result of the summation is in the range of -1 to 1.

We leave the creation of the triangle wave as a MATLAB exercise.

[wpfilebase tag=file id=51 tpl=supplement /]

If you actually want to hear one of these waves, you can generate the array of audio samples with

s = 1;

sr = 44100;

t = linspace(0, s, sr*s);

y = sawtooth(262*2*pi*t);

and then play the wave with

sound(y, sr);

It’s informative to create and listen to square, sawtooth, and triangle waves of various amplitudes and frequencies. This gives you some insight into how these waves can be used in sound synthesizers to mimic the sounds of various instruments. We’ll cover this in more detail in Chapter 6.

In this chapter, all our MATLAB examples are done by means of expressions that are evaluated directly from MATLAB’s command line. Another way to approach the problems is to write programs in MATLAB’s scripting language. We leave it to the reader to explore MATLAB script programming, and we’ll have examples in later chapters.

In the previous sections, we generated sine waves to generate sound data and manipulate it in various ways.  This is useful for understanding basic concepts regarding sound.  However, in practice you have real-world sounds that have been captured and stored in digital form.  Let’s look now at how we can read audio files in MATLAB and perform operations on them.

We’ve borrowed a short WAV file from Adobe Audition’s demo files, reducing it to mono rather than stereo.  MATLAB’s audioread function imports WAV files, as follows:

y = audioread('HornsE04Mono.wav');

This reads an array of audio samples into y, assuming that the file is in the current folder of MATLAB.  (You can set this through the Current Folder window at the top of MATLAB.)  If you want to know the sampling rate and bit depth (the number of bits per sample) of the audio file, you can get this information with

[y, sr, b] = audioread('HornsE04Mono.wav');

sr now contains the sampling rate and b contains the bit depth.  The Workspace window shows you the values in these variables.

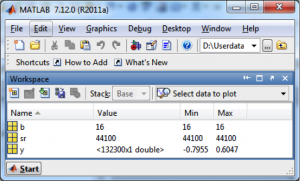
You can play the sound with

sound(y, sr);

Once you’ve read in a WAV file and have it stored in an array, you can easily do mathematical operations on it.  For example, you can make it quieter by multiplying by a number less than 1, as in

y = y * 0.5;

You can also write out the new form of the sound file, as in

audiowrite('HornsNew.wav', y, 44100);

In Section 2.2.3, we showed how sound can be represented graphically in two ways.  In the waveform view, time is on the horizontal axis and amplitude of the sound wave is on the vertical axis.  In the frequency analysis view, frequency is on the horizontal axis and the magnitude of the frequency component is on the vertical axis.  The waveform view represents sound in the time domain. The frequency analysis view represents sound in the frequency domain.  (See Figure 2.18 and Figure 2.19.)  Whether sound is represented in the time or the frequency domain, it’s just a list of numbers.  The information is essentially the same – it’s just that the way we look at it is different.

The one-dimensional Fourier transform is function that maps real to the complex numbers, given by the equation below.  It can be used to transform audio data from the time to the frequency domain.

[equation caption=”Equation 2.12 Fourier transform (continuous)”]

$$!F\left ( n \right )=\int_{-\infty }^{\infty }f\left ( k \right )e^{-i2\pi nk}dk\: where\: i=\sqrt{-1}$$

[/equation]

Sometimes it’s more convenient to represent sound data one way as opposed to another because it’s easier to manipulate it in a certain domain.  For example, in the time domain we can easily change the amplitude of the sound by multiplying each amplitude by a number.  On the other hand, it may be easier to eliminate certain frequencies or change the relative magnitudes of frequencies if we have the data represented in the frequency domain.

To be applied to discrete audio data, the Fourier transform must be rendered in a discrete form. This is given in the equation for the discrete Fourier transform below.

[equation caption=”Equation 2.13 Discrete Fourier transform”]

$$!F_{n}=\frac{1}{N}\left ( \sum_{k-0}^{N-1}f_{k}\cos \frac{2\pi nk}{N}-if_{k}\sin \frac{2\pi nk}{N} \right )=\frac{1}{N}\left ( \sum_{k=0}^{N-1}f_{k}e^{\frac{-i2\pi kn}{N}} \right )\mathrm{where}\; i=\sqrt{-1}$$

[/equation]

[aside]

The second form of the discrete Fourier transform given in Equation 2.1, $$\frac{1}{N}\left (\sum_{k=0}^{N-1}f_{k}e^{\frac{-i2\pi kn}{N}} \right )$$, uses the constant e.  It is derivable from the first by application of Euler’s identify, $$e^{i2\pi kn}=\cos \left ( 2\pi kn \right )+i\sin \left ( 2\pi kn \right )$$. To see the derivation, see (Burg 2008).

[/aside]

Notice that we’ve switched from the function notation used in Equation 2.12 ( $$F\left ( n \right )$$ and F\left ( k \right )) to array index notation in Equation 2.13 ( F_{n} and f_{k}) to emphasize that we are dealing with an array of discrete audio sample points in the time domain. Casting this equation as an algorithm (Algorithm 2.1) helps us to see how we could turn it into a computer program where the summation becomes a loop nested inside the outer for loop.

[equation caption=”Algorithm 2.1 Discrete Fourier transform” class=”algorithm”]

/*Input:

f, an array of digitized audio samples
N, the number of samples in the array
Note:  $$i=\sqrt{-1}$$

Output:

F, an array of complex numbers which give the frequency components of the sound given by f */

for (n = 0 to N – 1 )

$$F_{n}=\frac{1}{N}\left ( \sum \begin{matrix}N-1\\k=0 \end{matrix} f_{k}\, cos\frac{2\pi nk}{N}-if_{k}\, sin\frac{2\pi nk}{N}\right )$$

[/equation]

[wpfilebase tag=file id=149 tpl=supplement /]

[wpfilebase tag=file id=151 tpl=supplement /]

Each time through the loop, the magnitude and phase of the n^th frequency component are computed, $$F_{n}$$. Each $$F_{n}$$ is a complex number with a cosine and sine term, the sine term having the factor i in it.

We assume that you’re familiar with complex numbers, but if not, a short introduction should be enough so that you can work with the Fourier algorithm.

A complex number takes the form $$a+bi$$, where $$i=\sqrt{-1}$$. Thus,  $$cos\frac{2\pi nk}{N}-if_{k}\: sin\left ( \frac{2\pi nk}{N} \right )$$ is a complex number. In this case, a is replaced with $$cos\frac{2\pi nk}{N}$$ and b with $$-f_{k}\: sin\left ( \frac{2\pi nk}{N} \right )$$.  Handling the complex numbers in an implementation of the Fourier transform is not difficult. Although i is an imaginary number, $$\sqrt{-1}$$, and you might wonder how you’re supposed to do computation with it, you really don’t have to do anything with it at all except assume it’s there. The summation in the formula can be replaced by a loop that goes from 0 through N-1.   Each time through that loop, you add another term from the summation into an accumulating total. You can do this separately for the cosine and sine parts, setting aside i. Also, in object-oriented programming languages, you may have a Complex number class to do complex number calculations for you.

The result of the Fourier transform is a list of complex numbers F, each of the form $$a+bi$$, where the magnitude of the frequency component is equal to $$\sqrt{a^{2}+b^{2}}$$.

The inverse Fourier transform transforms audio data from the frequency domain to the time domain. The inverse discrete Fourier transform is given in Algorithm 6.2.

[equation caption=”Algorithm 2.2 Inverse discrete Fourier transform” class=”algorithm”]

/*Input:

F, an array of complex numbers representing audio data in the frequency domain, the elements represented by the coefficients of their real and imaginary parts, a and b respectively N, the number of samples in the array

Note: $$i=\sqrt{-1}$$

Output: f, an array of audio samples in the time domain*/

for $$(n=0 to N-1)$$

$$f_{k}=\sum \begin{matrix}N-1\\ n=0\end{matrix}\left ( a_{n}cos\frac{2\pi nk}{N}+ib_{n}sin\frac{2\pi nk}{N} \right )$$

[/equation]

If you know how to program, it’s not difficult to write your own discrete Fourier transform and its inverse through a literal implementation of the equations above.  However, the “literal” implementation of the transform is computationally expensive.  The equation in Algorithm 2.1 has to be applied N times, where N is the number of audio samples.  The equation itself has a summation that goes over N elements.  Thus, the discrete Fourier transform takes on the order of  $$N^{2}$$ operations.

[wpfilebase tag=file id=160 tpl=supplement /]

The fast Fourier transform (FFT) is a more efficient implementation of the Fourier transform that does on the order of  $$N\ast log_{2}N$$ operations.  The algorithm is made more efficient by eliminating duplicate mathematical operations.  The FFT is the version of the Fourier transform that you’ll often see in audio software and applications.  For example, Adobe Audition uses the FFT to generate its frequency analysis view, as shown in Figure 2.41.