3.1.6.1 Historical Context
For as far back in history as we can see, we find evidence that human beings have made music. We know this from ancient drawings of lutes and harps, Biblical references to David playing the lyre for King Saul, and the Greek philosopher Pythagoras’s calculation of harmonic intervals. The history of music and musical styles is a fascinating evolution of classical forms, prescriptive styles, breaks from tradition, and individual creativity. An important thread woven through this evolution is the mathematical basis of music and its relationship with beauty.
In the 6th century BC, the Greek philosopher Pythagoras recognized the mathematical basis of harmony, noting how the sound of a plucked string changes in proportion to the length of the string. However, harmony was not the most important element of music composition as it developed through the Middle Ages. The chanting of medieval monks evolved in a variety of styles and modalities. The early chants, called plainchant, were essentially syllabically-accented speech. Later styles involved two to eight monks chanting multiple melodic lines, traditionally with no instrumental accompaniment and in different musical modes. Madrigals of the Middle Ages were composed of single solo lines with simple instrumental accompaniment. In the Baroque period, multiple independent strands became interwoven in a style called polyphony, which reached its zenith in the fugues, canons, and contrapuntal compositions of Johann Sebastian Bach. Although we have come to think of harmony as an essential element of music, its music-theoretic development and its central position in music composition didn’t begin in earnest until the 18th century, spurred by Jean-Philippe Rameau’s Treatise on Harmony.
In this chapter, we emphasize the importance of harmony in musical composition because it is an essential feature of modern Western music. However, we acknowledge that perceptions of what is musical vary from era to era and culture to culture, and we can give only a small part of the picture here. We encourage the reader to explore other references on the subject of music history and theory for a more complete picture.
3.1.6.2 Intervals
An understanding of melody and harmony in Western music composition begins with intervals. An interval is the distance between two notes, measured by the number of lettered notes it contains counting both the starting and ending notes. If the notes are played at the same time, the interval is a harmonic interval. If the notes are played one after the other, it is a melodic interval. If there are at least three notes played simultaneously, they constitute a chord. When notes are played at the same time, they are stacked up vertically on the staff. Figure 3.24 shows a harmonic interval, melodic interval, and chord.

Intervals are named by the number of lettered notes from the lowest to highest, inclusive. The name of the interval can be expressed as an ordinal number. For example, if the interval begins at F and ends in D, there are six lettered notes in the interval, F, G, A, B, C, and D. Thus, this interval is called a sixth. If the interval begins with C and ends in E, it is called a third, as shown in Figure 3.25 Note that in this regard the presences of sharps or flats isn’t significant. The interval between F and D is a sixth, as is the interval between F and D#.

Because there are eight notes in an octave, with the last letter repeated, there are eight intervals in an octave. These are shown in Figure 3.26, in the key of C. Each interval is constructed in turn by starting on the key note and moving up by zero lettered notes, one lettered note, two lettered notes, and on up to eight lettered notes. Moving up one lettered note means moving up to the next line or space on the staff.
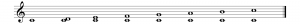
The same intervals can be created in any key. Consider the key of D. Unison is simply one note. A second is D an E. A third is D and F#. A fourth is D and G. A fifth is D and A. A sixth is D and B. A seventh is D and C#. These intervals are shown in Figure 3.27. Note that F and C are implicitly sharp in this key.
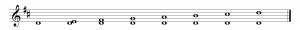
Intervals are named not only by their size but also by quality — major, perfect, minor, augmented, and diminished. A full discussion of the intervals qualities is beyond the scope of this book. We’ll introduce you to them by showing examples and explaining a little about how they relate to each other. (See Figure 3.28.)
A major interval is considered major if the second note of the interval is in the diatonic scale of a major scale beginning at the first note of the interval. For example, C and G constitute a major interval because G is a note in the key of C.
A major interval can be converted to a minor interval by lowering the higher note one semitone.
The intervals that cannot be made minor are called perfect. (They cannot be made minor because lowering the top note by a semitone creates a different interval. (For example, consider lowering the G in the C-G fifth by a semitone. Then the top note is an F, the interval becomes a fourth instead of a fifth.) The perfect intervals are perfect unison, the fourth, the fifth, and the octave.
Two other types of intervals exist: diminished and augmented. A diminished interval is one semitone smaller than a perfect interval or two semitones smaller than a major interval. An augmented interval is one semitone larger than a perfect or major interval. All the intervals for the key of C are shown in Figure 3.28. The intervals for other keys could be illustrated similarly.

You can create a compound interval by taking any of the interval types defined above and moving the upper note up by one or more octaves. If you’re trying to identify intervals in a score, you can count the number of lettered notes from the beginning to the end of the interval and “mod” that number by 7. The result gives you the type of interval. For example, if the remainder is 3, then the interval is a third. The mod operation divides by an integer and gives the remainder. This is the same as repeatedly subtracting 7 (the number of notes in an octave, not counting the repeat of the first note an octave higher) until you reach a number that is less than 7. Figure 3.29 shows examples of two compound intervals. The first goes from C4 to G5, a span of 12 notes. 12 mod 7 = 5, so this is a compound perfect fifth. The second interval goes from E4 to G5#, a span of 10 notes. 10 mod 7 = 3, so this is a compound third. However, because the G is raised to G#, this is, more precisely, a compound augmented third.

Intervals can be characterized as either consonant or dissonant. Giving an oversimplified definition, we can say that sounds that are pleasing to the ear are called consonant, and those that are not are called dissonant. Of course, these qualities are subjective. Throughout the history of music, the terms consonant and dissonant have undergone much discussion. Some music theorists would define consonance as a state when things are in accord with each other, and dissonance as a state of instability or tension that calls for resolution. In Section 3.3.2, we’ll look more closely at a physical and mathematical explanation for the subjective perception of consonance as it relates to harmony.
[wpfilebase tag=file id=34 tpl=supplement /]
Intervals help us to characterize the patterns of notes in a musical composition. The musical conventions from different cultures vary not only in their basic scales but also in the intervals that are agreed upon as pleasing to the ear. In Western music of our times, the perfect intervals, major and minor thirds, and major and minor sixths are generally considered consonant, while the seconds, sevenths, augmented, and diminished intervals are considered dissonant. The consonant intervals come to be used frequently in musical compositions of a culture, and the listener’s enjoyment is enhanced by a sense of recognition. This is not to say that dissonant intervals are simply ugly and never used. It is the combination of intervals that makes a composition. The combination of consonant and dissonant intervals gives the listener an alternating sense of tension and resolution, expectation and completion in a musical composition.
3.1.6.3 Chords
A chord is three or more notes played at the same time. We will look at the most basic chords here – triads, which consist of three notes stacked vertically in thirds, creating tertian harmony .
Triads can be major, minor, diminished, or augmented. The lowest note of a triad is its root. In a major triad, the second note is a major third above the root, and the third note is a perfect fifth above the root. In the root position of a triad in a given key, the tonic note of the key is the root of the triad. (Refer to Table 3.2 for the names of the notes in a diatonic scale.) The major triads for the keys of C, F, and A are shown in root position in Figure 3.30.

In a minor triad, the second note is a diatonic minor third above the root, and the third note is a diatonic perfect fifth above the root. The minor triads for the keys of C, F, and A are shown in root position in Figure 3.31.

Chords can be inverted by rotating the notes up or down – in other words, making the 3rd or the 5th the bottom or lowest note. In the first inversion, the lowest note is the 3rd, and in the second inversion, the lowest note is the 5th. In the second inversion, the mediant of the key becomes the root and the tonic is moved up an octave. In the third inversion, the dominant of the key becomes the root, and both the mediant and tonic are moved up an octave. The first and inversions are shown in Figure 3.32.

A diminished triad has a root note followed by a minor third and a diminished fifth. An augmented triad has a root note followed by a major third and an augmented fifth. The diminished and augmented triads for the key of C are shown in Figure 3.33.

We’ve looked at only triads so far. However, chords with four notes are also used, including the major, minor, and dominant sevenths. The major seventh chord consists of the root, major third, perfect fifth, and major seventh. The minor seventh consists of the root, minor third, perfect fifth, and minor seventh. The dominant seventh consists of the root, major third, perfect fifth, and minor seventh. Dominant chords have three inversions. The dominant seventh for the key of C is shown with its inversions in Figure 3.34. (Note that B is flat in all the inversions.)

Thus we have seven basic chords that are used in musical compositions. These are summarized in Table 3.9.
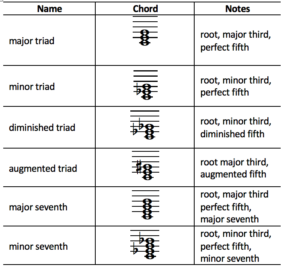
[wpfilebase tag=file id=113 tpl=supplement /]
All major keys give rise to a sequence of triads following the same pattern. To see this, consider the sequence you get in the key of C major by playing a triad starting on each of the piano keys in the scale. These triads are shown in Figure 3.35. Each is named with the name of its root note. (Note that we use the convention where upper case Roman numerals are used for major chords and lower case are used to minor chords. =)

[wpfilebase tag=file id=114 tpl=supplement /]
Each of the chords in this sequence can be characterized based on its root note. Triad I is easy to see. The first note is C and it’s a major triad, so it’s C major. Triad ii starts on D, so consider what kind of triad this would be in the key of D. It has the notes D, F, and A. However, in the key of D, F should be sharp. D is not sharp in the triad ii shown, so this is a minor triad from the key of D. Triad iii has the notes E, G, and B. In the key of E, G is sharp, but in the triad iii shown, it is not. Thus, the third triad in the key of C is E minor. Let’s skip to vii°, which has the notes B, D, and F. In the key of B, the notes D and F are sharp, but they’re not in triad vii. This makes vii° a B diminished. By this analysis, we can determine that the sequence of chords in C major is C major, D minor, E minor, F major, G major, A minor, and B diminished.
All major keys have this same sequence of chord types – major, minor, minor, major, major, minor, and diminished. For example, the key of D has the chords D major, E minor, F# minor, G major, A major, B minor and C# diminished. We refer you to a music theory textbook for a similar analysis of chords in a minor key.
[table caption=”Table 3.10 Types of triad chords in major and minor keys” width=”80%” colalign=”center|center|center”]
Chord~~number in~~major key,Chord~~type in major key, Chord number in~~minor key,Chord type~~inminor key
I,major,i,minor
ii,minor,ii°,diminished
iii,minor,III,major
IV,major,vi,minor
V,major,V,major
vi,minor,VI,major
vii°,diminished,vii°,diminished
[/table]
3.1.6.4 Chord Progressions
So what is the point of identifying and giving names to intervals and chords? The point is that this gives us a way to analyze music, communicate about it, and compose it in a way that yields a logical order and an aesthetically pleasing form within a style. When chords follow one another in certain progressions, they provoke feelings of tension and release, expectation and satisfaction, conflict and resolution. This emotional rhythm is basic to music composition.
Let’s look again at the chords playable in the key of C, as shown in Figure 3.35. Chord progressions can be represented by a sequence of Roman numerals that correspond to the scale degree (1 to 7) for the root note of the chord. For example, the right-hand part of “Twinkle, Twinkle Little Star” in the key of C major, shown in Figure 3.23, could be accompanied by the chords I I IV I IV I V I in the left hand, as shown in Figure 3.36. This chord progression is in fact a very common pattern.

You can play this yourself with reference to the triads from the key of C major, shown in Figure 3.35. However, to make the chords sound more interesting, you can invert them so that the lowest note leads more smoothly to the next chord’s lowest note (bass note). A beginning piano student may invert chords to make them easier to play. For example, chord I can be played as C, E, G; chord IV as C, F, A (2nd inversion); and chord V as B, D, G (1st inversion), as shown in Figure 3.37.

A simple way of looking at chord progressions is based on tonality – a system for defining the relationships of chords based on the tonic note for a given key. Recall that the tonic note is the note that begins the scale for a key. In fact, the key’s name is derived from the tonic note. In the key of C, the tonic note is C. Triad I is the tonic triad because it begins on the tonic note. You can think of this as the home chord, the chord where a song begins and to which it wants to return. Triad V is called the dominant chord. It has this name because chord progressions in a sense pull toward the dominant chord, but then tend to return to the home chord, chord I. Returning to chord I gives a sense of completion in a chord progression, called a cadence. The progression from I to V and back to I again is called an authentic cadence because it is the clearest example of tension and release in a chord progression. It is the most commonly used chord progression in modern popular music, and probably in Western music as a whole.
Another frequently used progression moves from I to IV and back to I. IV is the subdominant chord, named because it serves as a counterbalance to the dominant. The I IV I progression is called the plagal cadence. Churchgoers may recognize it as the sound of the closing “amen” to a hymn. Together, the tonic, subdominant, and dominant chords and their cadences serve as foundational chord progressions. You can see this in “Twinkle, Twinkle Little Star,” a tune for which Wolfgang Amadeus Mozart wrote twelve variations.
The perfect and plagal cadences are commonly used chord progressions, but they’re only the tip of the iceberg of possibilities. “Over the Rainbow” from The Wizard of Oz, with music written by Harold Arlen, is an example of how a small variation from the chord progression of “Twinkle, Twinkle Little Star” can yield beautiful results. If you speed up the tempo of “Over the Rainbow”, you can play it with the same chords as are used for “Twinkle, Twinkle Little Star,” as shown in Figure 3.38. The only one that sounds a bit “off” is the first IV.

[wpfilebase tag=file id=139 tpl=supplement /]
[wpfilebase tag=file id=140 tpl=supplement /]