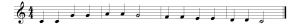3.1.5.1 Score
In the tradition of Western music, a system of symbols has been devised to communicate and preserve musical compositions. This system includes symbols for notes, timing, amplitude, and keys. A musical composition is notated on a score. There are scores of different types, depending on the instrument being played. The score we describe is for a standard piano, MIDI controller or keyboard score.
A piano score consists of two staves, each of which consists of five horizontal lines. The staves are drawn one above the other. The top staff is called the treble clef, representing the notes that are played by the right hand. The symbol for the treble clef is placed at the far left of the top staff. (The word “clef” is French for “key.”) The bottom staff is the bass clef, representing what is played with the left hand. The symbol for the bass clef is placed at the far left of the bottom staff. A blank score with no notes on it is pictured in Figure 3.10.
Each line and space on the treble and bass clef staves corresponds to a note on the keyboard to be played, as shown in Figure 3.11 and Figure 3.12. A whole note (defined below) is indicated by an oval like those shown. The letter for the corresponding note is given in the figures. The letters are ordinarily not shown on a musical score. We have them here for information only. The treble clef is sometimes called the G clef because its bottom portion curls around the line on the staff corresponding to the note G. The bass clef is sometimes called the F clef because it curls around the line on the staff corresponding to the note F.
It’s possible to place a note below or above one of the staves. The note’s distance from the staff indicates what note it is. If it’s a note that would fall on a line, a small line is placed through it, and if the note would fall on a space, a line is placed under or over it. The lines between the staff and the upper or lower note are displayed by a short line, also. The short lines that are used to extend the staff are called ledger lines. Examples of notes with ledger lines are shown in Figure 3.13 and Figure 3.14.
[wpfilebase tag=file id=33 tpl=supplement /]
Beginners who are learning to read music often use mnemonics to remember the notes corresponding to lines and spaces on a staff. For example, the lines on the treble clef staff, in ascending order, correspond to the notes E, G, B, D, and F, which can be memorized with the mnemonic “every good boy does fine.” The spaces on the treble clef staff, in ascending order, spell the word FACE. On the bass clef, the notes G, B, D, F, and A can be remembered as “good boys deserve favor always,” and the spaces A, C, E, G can be remembered as “a cow eats grass” (or whatever mnemonics you like).
3.1.5.2 Notes and their Durations
There are types of notes – whole notes, half notes, quarter notes, and so forth, as shown in Table 3.3. On the score, you can tell what type a note is by its shape and whether or not the note is filled in (black or white). The durations of notes are defined relative to each other, as you can see in the table. We could continue to create smaller and smaller notes, beyond those listed in the table, by adding more flags to a note. The part of the note called the flag is shown in Figure 3.15. Each time we add a flag, we divide the duration of the previously defined note by 2.
3.1.5.3 Rhythm, Tempo, and Meter
[wpfilebase tag=file id=109 tpl=supplement /]
The timing of a musical composition and its performance is a matter of meter, tempo, and rhythm.
Meter is the regular grouping of beats and placement of accents in notes. Since the duration of different notes are defined relative to each other, we have to have a baseline. This is given in a score’s time signature (a synonym of meter), which indicates which type of note gets one beat (quarter note, eighth note, etc.). (There are two types of meter – simple and compound. We are considering only simple meter here.)
Beats and notes are grouped into measures. Measures are sometimes called bars because they are separated from each other on the staff by a vertical line called a bar line.
A time signature of $$\frac{x}{y}$$, where x and y are integers, indicates that there are x beats to a measure, and a note of size $$\frac{1}{y}$$gets one beat. (A half note is size ½, a quarter note is size ¼, and so forth.) A time signature of $$\frac{4}{4}$$ time is shown in Figure 3.16, indicating four beats to a measure with a quarter note getting one beat. A time signature of $$\frac{3}{4}$$ indicates three beats to a measure with a quarter note getting one beat. $$\frac{3}{4}$$ is the meter for a waltz.
If the time signature of a piece is $$\frac{4}{4}$$, then there are four beats to a measure and each quarter note gets a beat. Consider the score in Figure 3.17, which shows you how to play “Twinkle, Twinkle Little Star” in $$\frac{4}{4}$$time in the key of C. Each of the six syllables in “Twin-kle Twin-kle Lit-tle” corresponds to a quarter note, and each is given equal time – one beat – in the first measure. Then the note corresponding to the word “star” is held for two beats in the second measure. Measures three and four are similar to measures one and two.
Tempo is the pace at which music is performed. We can sing “Yankee Doodle” in a fast, snappy pace or slowly, like a dirge. Obviously, most songs have tempos that seem more appropriate for them.
The tempo of a musical piece depends on which type of note is given one beat and how many beats there are per second. Tempo can be expressed at the beginning of the score explicitly, in terms of beats per minute (BPM). For example, a marking such as bpm = 72, ♩ = 72, or mm = 72 (for Maezel’s metronome) placed above a measure indicates that a tempo of 72 beats per minute is recommend from this point on, with a quarter note getting one beat. Alternatively, an Italian key word like allegro or andante can be used to indicate the beats per minute in a way that can be interpreted more subjectively. A list of some of these tempo markings is given in Table 3.4.
[table caption=”Table 3.4″ width=”80%” colalign=”center|center”]
Tempo Marking,Meaning
prestissimo,extremely fast (more than 200 BPM)
presto,very fast (168 – 200 BPM)
allegro,fast (120 – 168 BPM)
moderato,moderately (108 – 120 BPM)
andante,“at a walking pace” (76 – 108 BPM)
adagio,slowly (66 – 76 BPM)
lento or largo,very slowly (40 – 60 BPM)
[/table]
Students learning to play the piano sometimes use a device called a metronome to tick out the beats per minute while they practice (also known as a click). Metronomes are also usually built into MIDI sequencers and keyboards.
The Google dictionary gives three definitions of rhythm:
- a strong, regular, repeated pattern of movement or sound;
- the systematic arrangement of musical sounds, principally according to duration and periodic stress; and
- a particular type of pattern formed by rhythm.
You can see from these definitions that rhythm generally is based on the arrangement of notes of different durations that are sounded over time. Rhythm also includes the accenting of notes, which generally has a pattern. An example of this aspect of rhythm is illustrated by the rhythm of the message SOS in Morse code.
Rhythm and meter are interrelated. Meter is the macro-pattern of beats and accents that remains consistent throughout the song. Rhythm is the micro-pattern that gives the song its individuality. Once the meter is set for a section of a musical composition, the number of beats per measure must fit within that time signature. However, which particular types of rests and notes — whole, half, quarter, eighth, etc. — are chosen to add up to the number of beats per measure is up to the composer.
Rhythm is a complicated feature of music and is difficult to define in a general sense because of its many variations, so we won’t go into detail about it here.
3.1.5.4 Rests and their Durations
[wpfilebase tag=file id=138 tpl=supplement /]
The duration of silence between notes is indicated by a rest. The symbols for rests are given in Table 3.5. The length of a rest corresponds to the length of a note of the same name.
A dot placed after a note or rest increases its duration by one-half of its original value. This is shown in Table 3.6. Figure 3.18 shows a fragment of Mozart’s “A Little Night Music,” which contains eighth rests in the second, third, and fourth measures. Since this piece is in $$\frac{6}{8}$$ time, the eighth rest gets one beat.
3.1.5.5 Key Signature
Many words in the field of music and sound are overloaded – that is, they have different meanings in different contexts. The word “key” is one of these overloaded terms. Thus far, we have been using the word “key” to denote a physical key on the piano keyboard. (For the discussion that follows, we’ll call this kind of key a “piano key.”) There’s another denotation for key that relates to diatonic scales, both major and minor. In this usage of the word, a key is a group of notes that constitute a diatonic scale, whether major or minor.
Each key is named by the note on which it begins. The beginning note is called the key note or tonic ( tonal center) note. If we start a major diatonic scale on the piano key of C, then following the pattern 2 2 1 2 2 2 1, only white keys are played. This group of notes defines the key of C major. Now consider what happens if we start on the note D. If you look at the keyboard and consider playing only white keys starting with D, you can see that the pattern would be 2 1 2 2 2 1 2, not the 2 2 1 2 2 2 1 pattern we want for a major scale. Raising F and C each by a semitone – that is, making them F# and C# – changes the pattern to 2 2 1 2 2 2 1. Thus the notes D, E, F#, G, A, B, C# and D define the key of D. By this analysis, we see that the key of D requires two sharps – F and C. Similarly, if we start on D and follow the pattern for a minor diatonic scale – 2 1 2 2 1 2 2 – we play the notes D, E, F, G, A, B♭, and D. This is the key of D minor.
Each beginning note (tonic note) determines the number of sharps or flats that are played in the 2 2 1 2 2 2 1 scale for a major key or in the 2 1 2 2 1 2 2 sequence for a minor key. Beginning an octave on the piano key C implies you’re playing in the key of C and play no sharps or flats for C major. Beginning a scale on the piano key D implies that you’re playing in the key of D and play two sharps for D major.
Let’s try a similar analysis on the key of F. If you play a major scale starting on F using all white keys, you don’t get the pattern 2 2 1 2 2 2 1. The only way to get that pattern is to lower the fourth note, B, to B♭. Thus, the key of F major has one flat. The key of F minor has four flats – A♭, B♭, D♭, and E♭, as you can verify by following the sequence 2 1 2 2 1 2 2 starting on F.
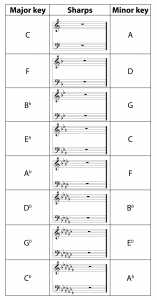
Like meter, the key of a musical composition is indicated at the beginning of each staff, in the key signature. The key signature indicates which notes are to be played as sharps or flats. The key signatures for all the major keys with sharps are given in Table 3.7. The key signatures for all the major keys with flats are given in Table 3.8.
You may have noticed that the keys of F major and D minor have the same key signature, each having one flat, B♭. So when you see the key signature for a musical composition and it has one flat in it, how do you know if the composition is written in F major or D minor, and what difference does it make? One difference lies in which note feels like the “home” note, the note to which the music wants to return to be at rest. A composition in the key of F major tends to begin and end in F. The use of specific chords reinforces the key, also. A second difference is a subjective response to major and minor keys. Minor keys generally sound more somber, sad, or serious while major keys are bright and happy to most listeners.
You can see in the tables below that each major key has a relative minor key, as indicated by the keys being in the same row in the table and sharing a key signature. Given a major key k, the relative minor is named by the note that is three semitones below k. For example, A is three semitones below C, and thus A is the relative minor key with respect to C major. When keys are described, if the words “major” and “minor” are not given, then the key is assumed to be a major key.
You’ve seen how, given the key note, you can determine the key signature for both major and minor keys. So how do you work in reverse? If you see the key signature, how can you tell what key this represents? A trick for major keys is to name the note that is one semitone above the last sharp in the key signature. For example, the last sharp in the second key signature in Table 3.7 is F#. One semitone above F# is G, and thus this is the key of G major. For minor keys, you name the note that is two semitones below the last sharp in the key signature. For the first key signature in Table 3.7, the last sharp is F#. Two semitones below this is the note E. Thus, this is also the key signature for E minor.
To determine a major key based on a key signature with flats, you name the note that is five semitones below the last flat. In the key that has three flats, the last flat is A♭. Five semitones below that is E♭, so this is the key of E♭major. (This turns out to be the next to last flat in each key with at least two flats.) To determine a minor key based on a key signature with flats, you name the note that is four semitones above the last flat. Thus, the key with three flats is the key of C minor. (You could also have gotten this by going three semitones down from the relative major key.)
The key signature for a harmonic minor key is the same as the natural minor. To create the pattern [2 1 2 2 1 3 1] (harmonic minor) from [2 1 2 2 1 2 2] (natural minor), the seventh scale degree is raised by a semitone. Since the natural minor’s key signature is being used, sharps or naturals are needed on individual notes to create the desired pattern of whole tones and semitones for the harmonic minor. The scale for a example harmonic minor is notated as shown in Figure 3.19. (In this section and following ones, we won’t include measures and time signatures when they are not important to the point being explained.)
Similarly, the melodic minor uses the key signature of the natural minor. Then adjustments have to be made in both the ascending and descending scales to create the melodic minor. To create the ascending pattern [2 1 2 2 2 2 1] (melodic minor) from [2 1 2 2 1 2 2] (natural minor), it suffices to raise both the sixth and seventh note by a semitone. This is done by adding sharps or naturals as necessary, depending on the key signature. The descending pattern for a melodic minor is the same as for the natural minor – [2 2 1 2 2 1 2]. Thus, the notes that are raised in the ascending scale have to be returned to their natural minor position for the key by adding flats, or naturals, as necessary. This is because once an accidental is added in a measure, it applies to the note to which it was added for the remainder of the measure.
F minor melodic is notated as shown in Figure 3.20. In F minor melodic, since D and E are normally flat for that key, a natural is added to each to remove the flat and thus move them up one semitone. Then in the descending scale, the D and E must explicitly be made flat again with the flat sign.
In E minor melodic, a sharp is added to the sixth and seventh notes – C and D – to raise them each as semitone. Then in the descending scale, the D and E must explicitly be made natural again with the sign, as shown in Figure 3.21.
3.1.5.6 The Circle of Fifths
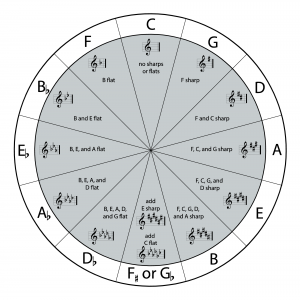
In Section 3.1.5, we showed how keys are distinguished by the sharps and flats they contain. One way to remember the keys is by means of the circle of fifths, a visual representation of the relationship among keys. The circle is shown in Figure 3.22. The outside of the circle indicates a certain key. The inner circle tells you how many sharps or flats are in the key.
[wpfilebase tag=file id=110 tpl=supplement /]
A fifth is a type of interval. We’ll discuss intervals in more detail in Section 3.1.6.2, but for now all you need to know that a fifth is a span of notes that includes five lettered notes. For example, the notes A, B, C, D, and E comprise a fifth, as do C, D, E, F, and G.
If you start with the key of C and move clockwise by intervals of fifths (which we call “counting up”), you reach successive keys each of which has one more sharp than the previous one – the keys of G, D, A, and so forth. For example, starting on C and count up a fifth, you move through C, D, E, F, and G, five lettered notes comprising a fifth. Counting up a fifth consists of moving up seven semitones – C to C#, C# to D, D to D#, D# to E, E to F, F to F#, and F# to G. Notice that on the circle, moving clockwise, you’re shown G as the next key up from the key of C. The key of G has one sharp. The next key up, moving by fifths, is the key of D, which has two sharps. You can continue counting up through the circle in this manner to find successive keys, each of which has one more sharp than the previous one.
Starting with the key of C and moving counterclockwise by intervals of fifths (“counting down”), you reach successive keys each of which has one more flat than the previous one – the keys of F, B♭, E♭, and so forth. Counting down a fifth from C takes you through C, B, A, G, and F – five lettered notes taking you through seven semitones, Counting down a fifth from F takes you through F, E, D, C, and B. However, since we again want to move seven semitones, the B is actually B♭. The seven semitones are F to E, E to E♭, E♭ to D, D to D♭, D♭ to C, C to B, and B to B♭. Thus, the key with two flats is the key of B♭.
[wpfilebase tag=file id=111 tpl=supplement /]
The keys shown in the circle of fifths are the same keys shown in Table 3.7 and Table 3.8. Theoretically, Table 3.7 could continue with keys that have seven sharps, eight sharps, and on infinitely. Moving the other direction, you could have keys with seven flats, eight flats, and on infinitely. These keys with an increasing number of sharps would continue to have equivalent keys with flats. We’ve shown in Figure 3.22 that the key of F#, with six sharps, is equivalent to the key of G♭, with six flats. We could have continued in this manner, showing that the key of C#, with seven sharps, is equivalent to the key of D♭, with five flats. Because the equivalent keys go on infinitely, the circle of fifths is sometimes represented as a spiral. Practically speaking, however, there’s little point in going beyond a key with six sharps or flats because such keys are harmonically the same as keys that could be represented with fewer accidentals. We leave it as an exercise for you to demonstrate to yourself the continued key equivalences.
3.1.5.7 Key Transposition
[wpfilebase tag=file id=112 tpl=supplement /]
All major keys have a similar sound in that the distance between neighboring notes on the scale follows the same pattern. One key is simply higher or lower than another. The same can be said for the similarity of minor keys. Thus, a musical piece can be transposed from one major (or minor) key to another without changing its composition. A singer might prefer one key over another because it is in the range of his or her voice.
Figure 3.23 shows the first seven notes of “Twinkle, Twinkle Little Star,” right-hand part only, transposed from the key of C major to the key of E major. If you play these on a keyboard, you’ll hear that C major and E major sound the same, except that the second is higher than the first.