2.1.1 Sound Waves, Sine Waves, and Harmonic Motion
Working with digital sound begins with an understanding of sound as a physical phenomenon. The sounds we hear are the result of vibrations of objects – for example, the human vocal chords, or the metal strings and wooden body of a guitar. In general, without the influence of a specific sound vibration, air molecules move around randomly. A vibrating object pushes against the randomly-moving air molecules in the vicinity of the vibrating object, causing them first to crowd together and then to move apart. The alternate crowding together and moving apart of these molecules in turn affects the surrounding air pressure. The air pressure around the vibrating object rises and falls in a regular pattern, and this fluctuation of air pressure, propagated outward, is what we hear as sound.
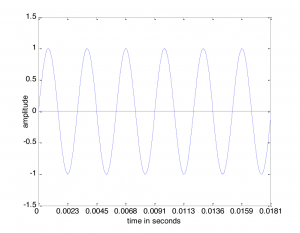
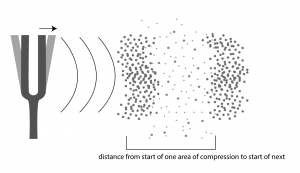
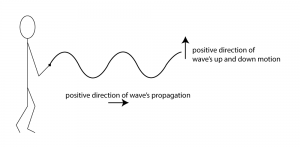
Sound is often referred to as a wave, but we need to be careful with the commonly-used term “sound wave,” as it can lead to a misconception about the nature of sound as a physical phenomenon. On the one hand, there’s the physical wave of energy passed through a medium as sound travels from its source to a listener. (We’ll assume for simplicity that the sound is traveling through air, although it can travel through other media.) Related to this is the graphical view of sound, a plot of air pressure amplitude at a particular position in space as it changes over time. For single-frequency sounds, this graph takes the shape of a “wave,” as shown in Figure 2.1. More precisely, a single-frequency sound can be expressed as a sine function and graphed as a sine wave (as we’ll describe in more detail later). Let’s see how these two things are related.
[wpfilebase tag=file id=105 tpl=supplement /]
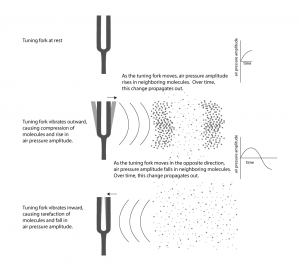
First, consider a very simple vibrating object – a tuning fork. When the tuning fork is struck, it begins to move back and forth. As the prong of the tuning fork vibrates outward (in Figure 2.2), it pushes the air molecules right next to it, which results in a rise in air pressure corresponding to a local increase in air density. This is called compression. Now, consider what happens when the prong vibrates inward. The air molecules have more room to spread out again, so the air pressure beside the tuning fork falls. The spreading out of the molecules is called decompression or rarefaction. A wave of rising and falling air pressure is transmitted to the listener’s ear. This is the physical phenomenon of sound, the actual sound wave.
Assume that a tuning fork creates a single-frequency wave. Such a sound wave can be graphed as a sine wave, as illustrated in Figure 2.1. An incorrect understanding of this graph would be to picture air molecules going up and down as they travel across space from the place in which the sound originates to the place in which it is heard. This would be as if a particular molecule starts out where the sound originates and ends up in the listener’s ear. This is not what is being pictured in a graph of a sound wave. It is the energy, not the air molecules themselves, that is being transmitted from the source of a sound to the listener’s ear. If the wave in Figure 2.1 is intended to depict a single-frequency sound wave, then the graph has time on the x-axis (the horizontal axis) and air pressure amplitude on the y-axis. As described above, the air pressure rises and falls. For a single-frequency sound wave, the rate at which it does this is regular and continuous, taking the shape of a sine wave.
Thus, the graph of a sound wave is a simple sine wave only if the sound has only one frequency component in it – that is, just one pitch. Most sounds are composed of multiple frequency components – multiple pitches. A sound with multiple frequency components also can be represented as a graph which plots amplitude over time; it’s just a graph with a more complicated shape. For simplicity, we sometimes use the term “sound wave” rather than “graph of a sound wave” for such graphs, assuming that you understand the difference between the physical phenomenon and the graph representing it.
The regular pattern of compression and rarefaction described above is an example of harmonic motion, also called harmonic oscillation. Another example of harmonic motion is a spring dangling vertically. If you pull on the bottom of the spring, it will bounce up and down in a regular pattern. Its position – that is, its displacement from its natural resting position – can be graphed over time in the same way that a sound wave’s air pressure amplitude can be graphed over time. The spring’s position increases as the spring stretches downward, and it goes to negative values as it bounces upwards. The speed of the spring’s motion slows down as it reaches its maximum extension, and then it speeds up again as it bounces upwards. This slowing down and speeding up as the spring bounces up and down can be modeled by the curve of a sine wave. In the ideal model, with no friction, the bouncing would go on forever. In reality, however, friction causes a damping effect such that the spring eventually comes to rest. We’ll discuss damping more in a later chapter.
Now consider how sound travels from one location to another. The first molecules bump into the molecules beside them, and they bump into the next ones, and so forth as time goes on. It’s something like a chain reaction of cars bumping into one another in a pile-up wreck. They don’t all hit each other simultaneously. The first hits the second, the second hits the third, and so on. In the case of sound waves, this passing along of the change in air pressure is called sound wave propagation. The movement of the air molecules is different from the chain reaction pile up of cars, however, in that the molecules vibrate back and forth. When the molecules vibrate in the direction opposite of their original direction, the drop in air pressure amplitude is propagated through space in the same way that the increase was propagated.
Be careful not to confuse the speed at which a sound wave propagates and the rate at which the air pressure amplitude changes from highest to lowest. The speed at which the sound is transmitted from the source of the sound to the listener of the sound is the speed of sound. The rate at which the air pressure changes at a given point in space – i.e., vibrates back and forth – is the frequency of the sound wave. You may understand this better through the following analogy. Imagine that you’re watching someone turn a flashlight on and off, repeatedly, at a certain fixed rate in order to communicate a sequence of numbers to you in binary code. The image of this person is transmitted to your eyes at the speed of light, analogous to the speed of sound. The rate at which the person is turning the flashlight on and off is the frequency of the communication, analogous to the frequency of a sound wave.
The above description of a sound wave implies that there must be a medium through which the changing pressure propagates. We’ve described sound traveling through air, but sound also can travel through liquids and solids. The speed at which the change in pressure propagates is the speed of sound. The speed of sound is different depending upon the medium in which sound is transmitted. It also varies by temperature and density. The speed of sound in air is approximately 1130 ft/s (or 344 m/s). Table 2.1 shows the approximate speed in other media.
[table caption=”Table 2.1 The Speed of sound in various media” colalign=”center|center|center” width=”80%”]
Medium,Speed of sound in m/s, Speed of sound in ft/s
“air (20° C, which is 68° F)”,344,”1,130″
“water (just above 0° C, which is 32° F)”,”1,410″,”4,626″
steel,”5,100″,”16,700″
lead,”1,210″,”3,970″
glass,”approximately 4,000~~(depending on type of glass)”,”approximately 13,200″
[/table]
[aside width=”75px”]
feet = ft
seconds = s
meters = m
[/aside]
For clarity, we’ve thus far simplified the picture of how sound propagates. Figure 2.2 makes it look as though there’s a single line of sound going straight out from the tuning fork and arriving at the listener’s ear. In fact, sound radiates out from a source at all angles in a sphere. Figure 2.3 shows a top-view image of a real sound radiation pattern, generated by software that uses sound dispersion data, measured from an actual loudspeaker, to predict how sound will propagate in a given three-dimensional space. In this case, we’re looking at the horizontal dispersion of the loudspeaker. Colors are used to indicate the amplitude of sound, going highest to lowest from red to yellow to green to blue. The figure shows that the amplitude of the sound is highest in front of the loudspeaker and lowest behind it. The simplification in Figure 2.2 suffices to give you a basic concept of sound as it emanates from a source and arrives at your ear. Later, when we begin to talk about acoustics, we’ll consider a more complete picture of sound waves.

Sound waves are passed through the ear canal to the eardrum, causing vibrations which pass to little hairs in the inner ear. These hairs are connected to the auditory nerve, which sends the signal onto the brain. The rate of a sound vibration – its frequency – is perceived as its pitch by the brain. The graph of a sound wave represents the changes in air pressure over time resulting from a vibrating source. To understand this better, let’s look more closely at the concept of frequency and other properties of sine waves.
2.1.2 Properties of Sine Waves
We assume that you have some familiarity with sine waves from trigonometry, but even if you don’t, you should be able to understand some basic concepts of this explanation.
A sine wave is a graph of a sine function . In the graph, the x-axis is the horizontal axis, and the y-axis is the vertical axis. A graph or phenomenon that takes the shape of a sine wave – oscillating up and down in a regular, continuous manner – is called a sinusoid.
In order to have the proper terminology to discuss sound waves and the corresponding sine functions, we need to take a little side trip into mathematics. We’ll first give the sine function as it applies to sound, and then we’ll explain the related terminology.
[equation caption=”Equation 2.1″]A single-frequency sound wave with frequency f , maximum amplitude A, and phase θ is represented by the sine function
$$!y=A\sin \left ( 2\pi fx+\theta \right )$$
where x is time and y is the amplitude of the sound wave at time x.[/equation]
[wpfilebase tag=file id=106 tpl=supplement /]
Single-frequency sound waves are sinusoidal waves. Although pure single-frequency sound waves do not occur naturally, they can be created artificially by means of a computer. Naturally occurring sound waves are combinations of frequency components, as we’ll discuss later in this chapter.
The graph of a sound wave is repeated Figure 2.4 with some of its parts labeled. The amplitude of a wave is its y value at some moment in time given by x. If we’re talking about a pure sine wave, then the wave’s amplitude, A, is the highest y value of the wave. We call this highest value the crest of the wave. The lowest value of the wave is called the trough. When we speak of the amplitude of the sine wave related to sound, we’re referring essentially to the change in air pressure caused by the vibrations that created the sound. This air pressure, which changes over time, can be measured in Newtons/meter2 or, more customarily, in decibels (abbreviated dB), a logarithmic unit explained in detail in Chapter 4. Amplitude is related to perceived loudness. The higher the amplitude of a sound wave, the louder it seems to the human ear.
In order to define frequency, we must first define a cycle. A cycle of a sine wave is a section of the wave from some starting position to the first moment at which it returns to that same position after having gone through its maximum and minimum amplitudes. Usually, we choose the starting position to be at some position where the wave crosses the x-axis, or zero crossing, so the cycle would be from that position to the next zero crossing where the wave starts to repeat, as shown in Figure 2.4.
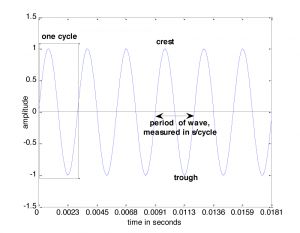
The frequency of a wave, f, is the number of cycles per unit time, customarily the number of cycles per second. A unit that is used in speaking of sound frequency is Hertz, defined as 1 cycle/second, and abbreviated Hz. In Figure 2.4, the time units on the x-axis are seconds. Thus, the frequency of the wave is 6 cycles/0.0181 seconds » 331 Hz. Henceforth, we’ll use the abbreviation s for seconds and ms for milliseconds.
Frequency is related to pitch in human perception. A single-frequency sound is perceived as a single pitch. For example, a sound wave of 440 Hz sounds like the note A on a piano (just above middle C). Humans hear in a frequency range of approximately 20 Hz to 20,000 Hz. The frequency ranges of most musical instruments fall between about 50 Hz and 5000 Hz. The range of frequencies that an individual can hear varies with age and other individual factors.
The period of a wave, T, is the time it takes for the wave to complete one cycle, measured in s/cycle. Frequency and period have an inverse relationship, given below.
[equation caption=”Equation 2.2″]Let the frequency of a sine wave be and f the period of a sine wave be T. Then
$$!f=1/T$$
and
$$!T=1/f$$
[/equation]
The period of the wave in Figure 2.4 is about three milliseconds per cycle. A 440 Hz wave (which has a frequency of 440 cycles/s) has a period of 1 s/440 cycles, which is about 0.00227 s/cycle. There are contexts in which it is more convenient to speak of period only in units of time, and in these contexts the “per cycle” can be omitted as long as units are handled consistently for a particular computation. With this in mind, a 440 Hz wave would simply be said to have a period of 2.27 milliseconds.
[wpfilebase tag=file id=28 tpl=supplement /]
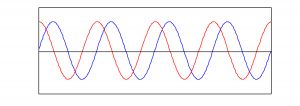
The phase of a wave, θ, is its offset from some specified starting position at x = 0. The sine of 0 is 0, so the blue graph in Figure 2.5 represents a sine function with no phase offset. However, consider a second sine wave with exactly the same frequency and amplitude, but displaced in the positive or negative direction on the x-axis relative to the first, as shown in Figure 2.5. The extent to which two waves have a phase offset relative to each other can be measured in degrees. If one sine wave is offset a full cycle from another, it has a 360 degree offset (denoted 360o); if it is offset a half cycle, is has a 180 o offset; if it is offset a quarter cycle, it has a 90 o offset, and so forth. In Figure 2.5, the red wave has a 90 o offset from the blue. Equivalently, you could say it has a 270 o offset, depending on whether you assume it is offset in the positive or negative x direction.
Wavelength, λ, is the distance that a single-frequency wave propagates in space as it completes one cycle. Another way to say this is that wavelength is the distance between a place where the air pressure is at its maximum and a neighboring place where it is at its maximum. Distance is not represented on the graph of a sound wave, so we cannot directly observe the wavelength on such a graph. Instead, we have to consider the relationship between the speed of sound and a particular sound wave’s period. Assume that the speed of sound is 1130 ft/s. If a 440 Hz wave takes 2.27 milliseconds to complete a cycle, then the position of maximum air pressure travels 1 cycle * 0.00227 s/cycle * 1130 ft/s in one wavelength, which is 2.57 ft. This relationship is given more generally in the equation below.
[equation caption=”Equation 2.3″]Let the frequency of a sine wave representing a sound be f, the period be T, the wavelength be λ, and the speed of sound be c. Then
$$!\lambda =cT$$
or equivalently
$$!\lambda =c/f$$
[/equation]
2.1.3 Longitudinal and Transverse Waves
[wpfilebase tag=file id=15 tpl=supplement /]
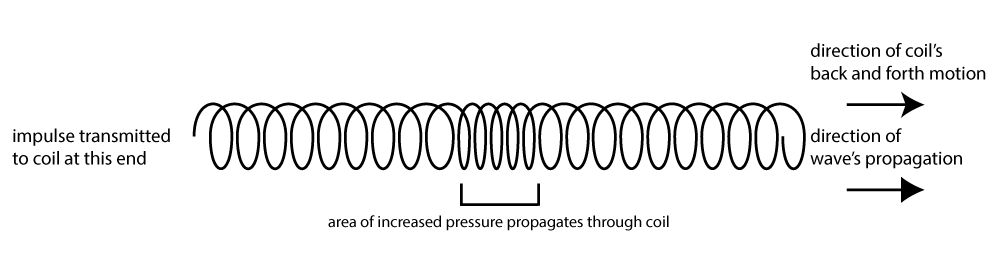
Sound waves are longitudinal waves. In a longitudinal wave, the displacement of the medium is parallel to the direction in which the wave propagates. For sound waves in air, air molecules are oscillating back and forth and propagating their energy in the same direction as their motion. You can picture a more concrete example if you remember the slinky toy of your childhood. If you and a friend lay a slinky along the floor and pull and push it back and forth, you create a longitudinal wave. The coils that make up the slinky are moving back and forth horizontally, in the same direction in which the wave propagates. The bouncing of a spring that is dangled vertically amounts to the same thing – a longitudinal wave.
[wpfilebase tag=file id=133 tpl=supplement /]
In contrast, in a transverse wave, the displacement of the medium is perpendicular to the direction in which the wave propagates. A jump rope shaken up and down is an example of a transverse wave. We call the quick shake that you give to the jump rope an impulse – like imparting a “bump” to the rope that propagates to the opposite end. The rope moves up and down, but the wave propagates from side to side, from one end of the rope to another. (You could also use your slinky to create a transverse wave, flipping it up and down rather than pushing and pulling it horizontally.)
2.1.4 Resonance
2.1.4.1 Resonance as Harmonic Frequencies
Have you ever heard someone use the expression, “That resonates with me”? A more informal version of this might be “That rings my bell.” What they mean by these expressions is that an object or event stirs something essential in their nature. This is a metaphoric use of the concept of resonance.
Resonance is an object’s tendency to vibrate or oscillate at a certain frequency that is basic to its nature. These vibrations can be excited in the presence of a stimulating force – like the ringing of a bell – or even in the presence of a frequency that sets it off – like glass shattering when just the right high-pitched note is sung. Musical instruments have natural resonant frequencies. When they are plucked, blown into, or struck, they vibrate at these resonant frequencies and resist others.
[wpfilebase tag=file id=107 tpl=supplement /]
Resonance results from an object’s shape, material, tension, and other physical properties. An object with resonance – for example, a musical instrument – vibrates at natural resonant frequencies consisting of a fundamental frequency and the related harmonic frequencies, all of which give an instrument its characteristic sound. The fundamental and harmonic frequencies are also referred to as the partials, since together they make up the full sound of the resonating object. The harmonic frequencies beyond the fundamental are called overtones. These terms can be slightly confusing. The fundamental frequency is the first harmonic because this frequency is one times itself. The frequency that is twice the fundamental is called the second harmonic or, equivalently, the first overtone. The frequency that is three times the fundamental is called the third harmonic or second overtone, and so forth. The number of harmonic frequencies depends upon the properties of the vibrating object.
One simple way to understand the sense in which a frequency might be natural to an object is to picture pushing a child on a swing. If you push a swing when it is at the top of its arc, you’re pushing it at its resonant frequency, and you’ll get the best effect with your push. Imagine trying to push the swing at any other point in the arc. You would simply be fighting against the natural flow. Another way to illustrate resonance is by means of a simple transverse wave, as we’ll show in the next section.
2.1.4.2 Resonance of a Transverse Wave
[wpfilebase tag=file id=130 tpl=supplement /]
We can observe resonance in the example of a simple transverse wave that results from sending an impulse along a rope that is fixed at both ends. Imagine that you’re jerking the rope upward to create an impulse. The widest upward bump you could create in the rope would be the entire length of the rope. Since a wave consists of an upward movement followed by a downward movement, this impulse would represent half the total wavelength of the wave you’re transmitting. The full wavelength, twice the length of the rope, is conceptualized in Figure 2.9. This is the fundamental wavelength of the fixed-end transverse wave. The fundamental wavelength (along with the speed at which the wave is propagated down the rope) defines the fundamental frequency at which the shaken rope resonates.
[equation caption=”Equation 2.4″]If L is the length of a rope fixed at both ends, then λ is the fundamental wavelength of the rope, given by
$$!\lambda =2L$$
[/equation]

Now imagine that you and a friend are holding a rope between you and shaking it up and down. It’s possible to get the rope into a state of vibration where there are stationary points and other points between them where the rope vibrates up and down, as shown in Figure 2.10. This is called a standing wave. In order to get the rope into this state, you have to shake the rope at a resonant frequency. A rope can vibrate at more than one resonant frequency, each one giving rise to a specific mode – i.e., a pattern or shape of vibration. At its fundamental frequency, the whole rope is vibrating up and down (mode 1). Shaking at twice that rate excites the next resonant frequency of the rope, where one half of the rope is vibrating up while the other is vibrating down (mode 2). This is the second harmonic (first overtone) of the vibrating rope. In the third harmonic, the “up and down” vibrating areas constitute one third of the rope’s length each.
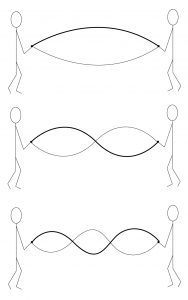
This phenomenon of a standing wave and resonant frequencies also manifests itself in a musical instrument. Suppose that instead of a rope, we have a guitar string fixed at both ends. Unlike the rope that is shaken at different rates of speed, guitar strings are plucked. This pluck, like an impulse, excites multiple resonant frequencies of the string at the same time, including the fundamental and any harmonics. The fundamental frequency of the guitar string results from the length of the string, the tension with which it is held between two fixed points, and the physical material of the string.
The harmonic modes of a string are depicted in Figure 2.11. The top picture in the figure illustrates the string vibrating according to its fundamental frequency. The wavelength l of the fundamental frequency is two times the length of the string L.
The second picture from the top in Figure 2.11 shows the second harmonic frequency of the string. Here, the wavelength is equal to the length of the string, and the corresponding frequency is twice the frequency of the fundamental. In the third harmonic frequency, the wavelength is 2/3 times the length of the string, and the corresponding frequency is three times the frequency of the fundamental. In the fourth harmonic frequency, the wavelength is 1/2 times the length of the string, and the corresponding frequency is four times the frequency of the fundamental. More harmonic frequencies could exist beyond this depending on the type of string.
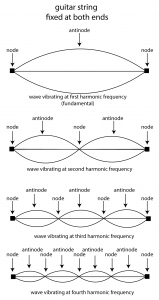
Like a rope held at both ends, a guitar string fixed at both ends creates a standing wave as it vibrates according to its resonant frequencies. In a standing wave, there exist points in the wave that don’t move. These are called the nodes, as pictured in Figure 2.11. The antinodes are the high and low points between which the string vibrates. This is hard to illustrate in a still image, but you should imagine the wave as if it’s anchored at the nodes and swinging back and forth between the nodes with high and low points at the antinodes.
It’s important to note that this figure illustrates the physical movement of the string, not a graph of a sine wave representing the string’s sound. The string’s vibration is in the form of a transverse wave, where the string moves up and down while the tensile energy of the string propagates perpendicular to the vibration. Sound is a longitudinal wave.
The speed of the wave’s propagation through the string is a function of the tension force on the string, the mass of the string, and the string’s length. If you have two strings of the same length and mass and one is stretched more tightly than another, it will have a higher wave propagation speed and thus a higher frequency. The frequency arises from the properties of the string, including its fundamental wavelength, 2L, and the extent to which it is stretched.
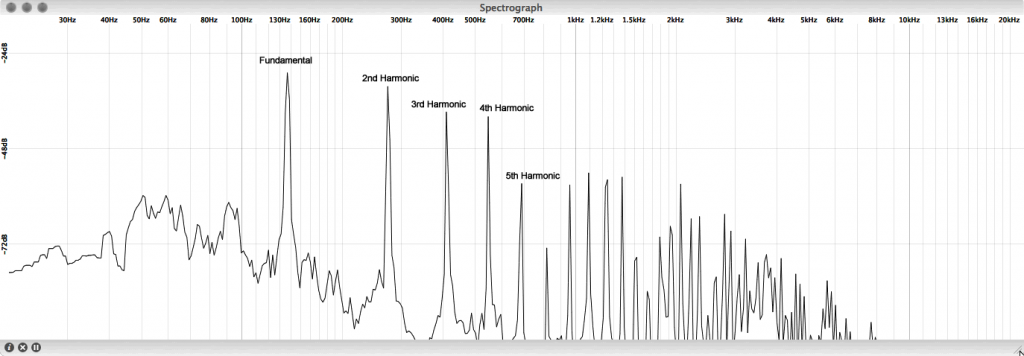
What is most significant is that you can hear the string as it vibrates at its resonant frequencies. These vibrations are transmitted to a resonant chamber, like a box, which in turn excites the neighboring air molecules. The excitation is propagated through the air as a transfer of energy in a longitudinal sound wave. The frequencies at which the string vibrates are translated into air pressure changes occurring with the same frequencies, and this creates the sound of the instrument. Figure 2.12 shows an example harmonic spectrum of a plucked guitar string. You can clearly see the resonant frequencies of the string, starting with the fundamental and increasing in integer multiples (twice the fundamental, three times the fundamental, etc.). It is interesting to note that not all the harmonics resonate with the same energy. Typically, the magnitude of the harmonics decreases as the frequency increases, where the fundamental is the most dominant. Also keep in mind that the harmonic spectrum and strength of the individual harmonics can vary somewhat depending on how the resonator is excited. How hard a string is plucked, or whether it is bowed or struck with a wooden stick or soft mallet, can have an effect on the way the object resonates and sounds.
2.1.4.3 Resonance of a Longitudinal Wave
[wpfilebase tag=file id=131 tpl=supplement /]
Not all musical instruments are made from strings. Many are constructed from cylindrical spaces of various types, like those found in clarinets, trombones, and trumpets. Let’s think of these cylindrical spaces in the abstract as a pipe.
A significant difference between the type of wave created from blowing air into a pipe and a wave created by plucking a string is that the wave in the pipe is longitudinal while the wave on the string is transverse. When air is blown into the end of a pipe, air pressure changes are propagated through the pipe to the opposite end. The direction in which the air molecules vibrate is parallel to the direction in which the wave propagates.
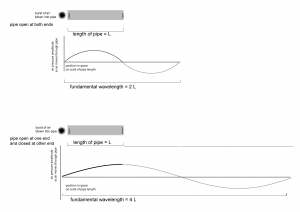
Consider first a pipe that is open at both ends. Imagine that a sudden pulse of air is sent through one of the open ends of the pipe. The air is at atmospheric pressure at both open ends of the pipe. As the air is blown into the end, the air pressure rises, reaching its maximum at the middle and falling to its minimum again at the other open end. This is shown in the top part of Figure 2.13. The figure shows that the resulting fundamental wavelength of sound produced in the pipe is twice the length of the pipe (similar to the guitar string fixed at both ends).
[wpfilebase tag=file id=13 tpl=supplement /]
The situation is different if the pipe is closed at the end opposite to the one into which it is blown. In this case, air pressure rises to its maximum at the closed end. The bottom part of Figure 2.13 shows that in this situation, the closed end corresponds to the crest of the fundamental wavelength. Thus, the fundamental wavelength is four times the length of the pipe.
Because the wave in the pipe is traveling through air, it is simply a sound wave, and thus we know its speed – approximately 1130 ft/s. With this information, we can calculate the fundamental frequency of both closed and open pipes, given their length.
[equation caption=”Equation 2.5″]Let L be the length of an open pipe, and let c be the speed of sound. Then the fundamental frequency of the pipe is.
$$!\frac{c}{2L}$$
[/equation]
[equation caption=”Equation 2.6″]Let L be the length of a closed pipe, and let c be the speed of sound. Then the fundamental frequency of the pipe is .
$$!\frac{c}{4L}$$
[/equation]
This explanation is intended to shed light on why each instrument has a characteristic sound, called its timbre. The timbre of an instrument is the sound that results from its fundamental frequency and the harmonic frequencies it produces, all of which are integer multiples of the fundamental. All the resonant frequencies of an instrument can be present simultaneously. They make up the frequency components of the sound emitted by the instrument. The components may be excited at a lower energy and fade out at different rates, however. Other frequencies contribute to the sound of an instrument as well, like the squeak of fingers moving across frets, the sound of a bow pulled across a string, or the frequencies produced by the resonant chamber of a guitar’s body. Instruments are also characterized by the way their amplitude changes over time when they are plucked, bowed, or blown into. The changes of amplitude are called the amplitude envelope, as we’ll discuss in a later section.
Resonance is one of the phenomena that gives musical instruments their characteristic sounds. Guitar strings alone do not make a very audible sound when plucked. However, when a guitar string is attached to a large wooden box with a shape and size that is proportional to the wavelengths of the frequencies generated by the string, the box resonates with the sound of the string in a way that makes it audible to a listener several feet away. Drumheads likewise do not make a very audible sound when hit with a stick. Attach the drumhead to a large box with a size and shape proportional to the diameter of the membrane, however, and the box resonates with the sound of that drumhead so it can be heard. Even wind instruments benefit from resonance. The wooden reed of a clarinet vibrating against a mouthpiece makes a fairly steady and quiet sound, but when that mouthpiece is attached to a tube, a frequency will resonate with a wavelength proportional to the length of the tube. Punching some holes in the tube that can be left open or covered in various combinations effectively changes the length of the tube and allows other frequencies to resonate.
2.1.5 Digitizing Sound Waves
In this chapter, we have been describing sound as continuous changes of air pressure amplitude. In this sense, sound is an analog phenomenon – a physical phenomenon that could be represented as continuously changing voltages. Computers require that we use a discrete representation of sound. In particular, when sound is captured as data in a computer, it is represented as a list of numbers. Capturing sound in a form that can be handled by a computer is a process called analog-to-digital conversion, whereby the amplitude of a sound wave is measured at evenly-spaced intervals in time – typically 44,100 times per second, or even more. Details of analog-to-digital conversion are covered in Chapter 5. For now, it suffices to think of digitized sound as a list of numbers. Once a computer has captured sound as a list of numbers, a whole host of mathematical operations can be performed on the sound to change its loudness, pitch, frequency balance, and so forth. We’ll begin to see how this works in the following sections.
4.1.1 Acoustics
The word acoustics has multiple definitions, all of them interrelated. In the most general sense, acoustics is the scientific study of sound, covering how sound is generated, transmitted, and received. Acoustics can also refer more specifically to the properties of a room that cause it to reflect, refract, and absorb sound. We can also use the term acoustics as the study of particular recordings or particular instances of sound and the analysis of their sonic characteristics. We’ll touch on all these meanings in this chapter.
4.1.2 Psychoacoustics
Human hearing is a wondrous creation that in some ways we understand very well, and in other ways we don’t understand at all. We can look at anatomy of the human ear and analyze – down to the level of tiny little hairs in the basilar membrane – how vibrations are received and transmitted through the nervous system. But how this communication is translated by the brain into the subjective experience of sound and music remains a mystery. (See (Levitin, 2007).)
We’ll probably never know how vibrations of air pressure are transformed into our marvelous experience of music and speech. Still, a great deal has been learned from an analysis of the interplay among physics, the human anatomy, and perception. This interplay is the realm of psychoacoustics, the scientific study of sound perception. Any number of sources can give you the details of the anatomy of the human ear and how it receives and processes sound waves. (Pohlman 2005), (Rossing, Moore, and Wheeler 2002), and (Everest and Pohlmann) are good sources, for example. In this chapter, we want to focus on the elements that shed light on best practices in recording, encoding, processing, compressing, and playing digital sound. Most important for our purposes is an examination of how humans subjectively perceive the frequencies, amplitude, and direction of sound. A concept that appears repeatedly in this context is the non-linear nature of human sound perception. Understanding this concept leads to a mathematical representation of sound that is modeled after the way we humans experience it, a representation well-suited for digital analysis and processing of sound, as we’ll see in what follows. First, we need to be clear about the language we use in describing sound.
4.1.3 Objective and Subjective Measures of Sound
In speaking of sound perception, it’s important to distinguish between words which describe objective measurements and those that describe subjective experience.
The terms intensity and pressure denote objective measurements that relate to our subjective experience of the loudness of sound. Intensity, as it relates to sound, is defined as the power carried by a sound wave per unit of area, expressed in watts per square meter (W/m2). Power is defined as energy per unit time, measured in watts (W). Power can also be defined as the rate at which work is performed or energy converted. Watts are used to measure the output of power amplifiers and the power handling levels of loudspeakers. Pressure is defined as force divided by the area over which it is distributed, measured in newtons per square meter (N/m2)or more simply, pascals (Pa). In relation to sound, we speak specifically of air pressure amplitude and measure it in pascals. Air pressure amplitude caused by sound waves is measured as a displacement above or below equilibrium atmospheric pressure. During audio recording, a microphone measures this constantly changing air pressure amplitude and converts it to electrical units of volts (V), sending the voltages to the sound card for analog-to-digital conversion. We’ll see below how and why all these units are converted to decibels.
The objective measures of intensity and air pressure amplitude relate to our subjective experience of the loudness of sound. Generally, the greater the intensity or pressure created by the sound waves, the louder this sounds to us. However, loudness can be measured only by subjective experience – that is, by an individual saying how loud the sound seems to him or her. The relationship between air pressure amplitude and loudness is not linear. That is, you can’t assume that if the pressure is doubled, the sound seems twice as loud. In fact, it takes about ten times the pressure for a sound to seem twice as loud. Further, our sensitivity to amplitude differences varies with frequencies, as we’ll discuss in more detail in Section 4.1.6.3.
When we speak of the amplitude of a sound, we’re speaking of the sound pressure displacement as compared to equilibrium atmospheric pressure. The range of the quietest to the loudest sounds in our comfortable hearing range is actually quite large. The loudest sounds are on the order of 20 Pa. The quietest are on the order of 20 μPa, which is 20 x 10-6 Pa. (These values vary by the frequencies that are heard.) Thus, the loudest has about 1,000,000 times more air pressure amplitude than the quietest. Since intensity is proportional to the square of pressure, the loudest sound we listen to (at the verge of hearing damage) is $$10^{6^{2}}=10^{12} =$$ 1,000,000,000,000 times more intense than the quietest. (Some sources even claim a factor of 10,000,000,000,000 between loudest and quietest intensities. It depends on what you consider the threshold of pain and hearing damage.) This is a wide dynamic range for human hearing.
Another subjective perception of sound is pitch. As you learned in Chapter 3, the pitch of a note is how “high” or “low” the note seems to you. The related objective measure is frequency. In general, the higher the frequency, the higher is the perceived pitch. But once again, the relationship between pitch and frequency is not linear, as you’ll see below. Also, our sensitivity to frequency-differences varies across the spectrum, and our perception of the pitch depends partly on how loud the sound is. A high pitch can seem to get higher when its loudness is increased, whereas a low pitch can seem to get lower. Context matters as well in that the pitch of a frequency may seem to shift when it is combined with other frequencies in a complex tone.
Let’s look at these elements of sound perception more closely.
4.1.4 Units for Measuring Electricity and Sound
In order to define decibels, which are used to measure sound loudness, we need to define some units that are used to measure electricity as well as acoustical power, intensity, and pressure.
Both analog and digital sound devices use electricity to represent and transmit sound. Electricity is the flow of electrons through wires and circuits. There are four interrelated components in electricity that are important to understand:
- potential energy (in electricity called voltage or electrical pressure, measured in volts, abbreviated V),
- intensity (in electricity called current, measured in amperes or amps, abbreviated A),
- resistance (measured in ohms, abbreviated Ω), and
- power (measured in watts, abbreviated W).
Electricity can be understood through an analogy with the flow of water (borrowed from (Thompson 2005)). Picture two tanks connected by a pipe. One tank has water in it; the other is empty. Potential energy is created by the presence of water in the first tank. The water flows through the pipe from the first tank to the second with some intensity. The pipe has a certain amount of resistance to the flow of water as a result of its physical properties, like its size. The potential energy provided by the full tank, reduced somewhat by the resistance of the pipe, results in the power of the water flowing through the pipe.
By analogy, in an electrical circuit we have two voltages connected by a conductor. Analogous to the full tank of water, we have a voltage – an excess of electrons – at one end of the circuit. Let’s say that at other end of the circuit we have 0 voltage, also called ground or ground potential. The voltage at the first end of the circuit causes pressure, or potential energy, as the excess electrons want to move toward ground. This flow of electricity is called the current. A electrical or digital circuit is a risky affair and only the experienced can handle such a complicated task at hand. It is essential that one goes through the right selection guide, like the Altera fpga selection guide and only then embark upon an ambitious project. If you are looking to save on your electric bill visit utilitysavingexpert.com. The physical connection between the two halves of the circuit provides resistance to the flow. The connection might be a copper wire, which offers little resistance and is thus called a good conductor. On the other hand, something could intentionally be inserted into the circuit to reduce the current – a resistor for example. The power in the circuit is determined by a combination of the voltage and the resistance.
The relationship among potential energy, intensity, resistance, and power are captured in Ohm’s law, which states that intensity (or current) is equal to potential energy (or voltage) divided by resistance:
[equation caption=”Equation 4.1 Ohm’s law”]
$$!i=\frac{V}{R}$$
where I is intensity, V is potential energy, and R is resistance
[/equation]
Power is defined as intensity multiplied by potential energy.
[equation caption=”Equation 4.2 Equation for power”]
$$!P=IV$$
where P is power, I is intensity, and V is potential energy
[/equation]
Combining the two equations above, we can represent power as follows:
[equation caption=”Equation 4.3 Equation for power in terms of voltage and resistance”]
$$!P=\frac{V^{2}}{R}$$
where P is power, V is potential energy, and R is resistance
[/equation]
Thus, if you know any two of these four values you can get the other two from the equations above.
Volts, amps, ohms, and watts are convenient units to measure potential energy, current resistance, and power in that they have the following relationship:
1 V across 1 Ω of resistance will generate 1 A of current and result in 1 W of power
The above discussion speaks of power (W), intensity (I), and potential energy (V) in the context of electricity. These words can also be used to describe acoustical power and intensity as well as the air pressure amplitude changes detected by microphones and translated to voltages. Power, intensity, and pressure are valid ways to measure sound as a physical phenomenon. However, decibels are more appropriate to represent the loudness of one sound relative to another, as well see in the next section.
4.1.5 Decibels
4.1.5.1 Why Decibels for Sound?
No doubt you’re familiar with the use of decibels related to sound, but let’s look more closely at the definition of decibels and why they are a good way to represent sound levels as they’re perceived by human ears.
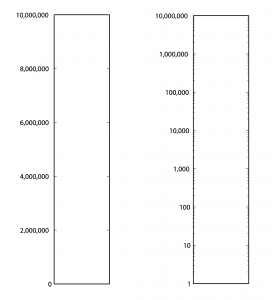
First consider Table 4.1. From column 3, you can see that the sound of a nearby jet engine has on the order of times greater air pressure amplitude than the threshold of hearing. That’s quite a wide range. Imagine a graph of sound loudness that has perceived loudness on the horizontal axis and air pressure amplitude on the vertical axis. We would need numbers ranging from 0 to 10,000,000 on the vertical axis (Figure 4.1). This axis would have to be compressed to fit on a sheet of paper or a computer screen, and we wouldn’t see much space between, say, 100 and 200. Thus, our ability to show small changes at low amplitude would not be great. Although we perceive a vacuum cleaner to be approximately twice as loud as normal conversation, we would hardly be able to see any difference between their respective air pressure amplitudes if we have to include such a wide range of numbers, spacing them evenly on what is called a linear scale. A linear scale turns out to be a very poor representation of human hearing. We humans can more easily distinguish the difference between two low amplitude sounds that are close in amplitude than we can distinguish between two high amplitude sounds that are close in amplitude. The linear scale for loudness doesn’t provide sufficient resolution at low amplitudes to show changes that might actually be perceptible to the human ear.
[table caption=”Table 4.1 Loudness of common sounds measured in air pressure amplitude and in decibels” width=”80%”]
Sound,Approximate Air Pressure~~Amplitude in Pascals,Ratio of Sound’s Air Pressure~~Amplitude to Air Pressure Amplitude~~of Threshold of Hearing,Approximate Loudness~~in dBSPL
Threshold of hearing,$$0.00002 = 2 \ast 10^{-5}$$ ,1,0
Breathing,$$0.00006325 = 6.325 \ast 10^{-5}$$ ,3.16,10
Rustling leaves,$$0.0002=2\ast 10^{-4}$$,10,20
Refrigerator humming,$$0.002 = 2 \ast 10^{-3}$$ ,$$10^{2}$$,40
Normal conversation,$$0.02 = 2\ast 10^{-2}$$ ,$$10^{3}$$,60
Vacuum cleaner,$$0.06325 =6.325 \ast 10^{-2}$$ ,$$3.16 \ast 10^{3}$$,70
Dishwasher,$$0.1125 = 1.125 \ast 10^{-1}$$,$$5.63 \ast 10^{3}$$,75
City traffic,$$0.2 = 2 \ast 10^{-1}$$,$$10^{4}$$,80
Lawnmower,$$0.3557 = 3.557 \ast 10^{-1}$$,$$1.78 \ast 10^{4}$$,85
Subway,$$0.6325 = 6.325 \ast 10^{-1}$$,$$3.16 \ast 10^{4}$$,90
Symphony orchestra,6.325,$$3.16 \ast 10^{5}$$,110
Fireworks,$$20 = 2 \ast 10^{1}$$,$$10^{6}$$,120
Rock concert,$$20+ = 2 \ast 10^{1}+$$,$$10^{6}+$$,120+
Shotgun firing,$$63.25 = 6.325 \ast 10^{1}$$,$$3.16 \ast 10^{6}$$,130
Jet engine close by,$$200 = 2 \ast 10^{2}$$,$$2 \ast 10^{7}$$,140
[/table]
Now let’s see how these observations begin to help us make sense of the decibel. A decibel is based on a ratio – that is, one value relative to another, as in $$\frac{X_{1}}{X_{0}}$$. Hypothetically, $$X_{0}$$ and $$X_{1}$$ could measure anything, as long as they measure the same type of thing in the same units – e.g., power, intensity, air pressure amplitude, noise on a computer network, loudspeaker efficiency, signal-to-noise ratio, etc. Because decibels are based on a ratio, they imply a comparison. Decibels can be a measure of
- a change from level $$X_{0}$$ to level $$X_{1}$$
- a range of values between $$X_{0}$$ and $$X_{1}$$, or
- a level $$X_{1}$$ compared to some agreed upon reference point $$X_{0}$$.
What we’re most interested in with regard to sound is some way of indicating how loud it seems to human ears. What if we were to measure relative loudness using the threshold of hearing as our point of comparison – the $$X_{0}$$, in the ratio $$\frac{X_{1}}{X_{0}}$$, as in column 3 of Table 4.1? That seems to make sense. But we already noted that the ratio of the loudest to the softest thing in our table is 10,000,000/1. A ratio alone isn’t enough to turn the range of human hearing into manageable numbers, nor does it account for the non-linearity of our perception.
The discussion above is given to explain why it makes sense to use the logarithm of the ratio of $$\frac{X_{1}}{X_{0}}$$ to express the loudness of sounds, as shown in Equation 4.4. Using the logarithm of the ratio, we don’t have to use such widely-ranging numbers to represent sound amplitudes, and we “stretch out” the distance between the values corresponding to low amplitude sounds, providing better resolution in this area.
The values in column 4 of Table 4.1, measuring sound loudness in decibels, come from the following equation for decibels-sound-pressure-level, abbreviated dBSPL.
[equation caption=”Equation 4.4 Definition of dBSPL, also called ΔVoltage”]
$$!dBSPL = \Delta Voltage \; dB=20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$
[/equation]
In this definition, $$V_{0}$$ is the air pressure amplitude at the threshold of hearing, and $$V_{1}$$ is the air pressure amplitude of the sound being measured.
Notice that in Equation 4.4, we use ΔVoltage dB as synonymous with dBSPL. This is because microphones measure sound as air pressure amplitudes, turn the measurements into voltages levels, and convey the voltage values to an audio interface for digitization. Thus, voltages are just another way of capturing air pressure amplitude.
Notice also that because the dimensions are the same in the numerator and denominator of $$\frac{V_{1}}{V_{0}}$$, the dimensions cancel in the ratio. This is always true for decibels. Because they are derived from a ratio, decibels are dimensionless units. Decibels aren’t volts or watts or pascals or newtons; they’re just the logarithm of a ratio.
Hypothetically, the decibel can be used to measure anything, but it’s most appropriate for physical phenomena that have a wide range of levels where the values grow exponentially relative to our perception of them. Power, intensity, and air pressure amplitude are three physical phenomena related to sound that can be measured with decibels. The important thing in any usage of the term decibels is that you know the reference point – the level that is in the denominator of the ratio. Different usages of the term decibel sometimes add different letters to the dB abbreviation to clarify the context, as in dBPWL (decibels-power-level), dBSIL (decibels-sound-intensity-level), and dBFS (decibels-full-scale), all of which are explained below.
Comparing the columns in Table 4.1, we now can see the advantages of decibels over air pressure amplitudes. If we had to graph loudness using Pa as our units, the scale would be so large that the first ten sound levels (from silence all the way up to subways) would not be distinguishable from 0 on the graph. With decibels, loudness levels that are easily distinguishable by the ear can be seen as such on the decibel scale.
Decibels are also more intuitively understandable than air pressure amplitudes as a way of talking about loudness changes. As you work with sound amplitudes measured in decibels, you’ll become familiar with some easy-to-remember relationships summarized in Table 4.2. In an acoustically-insulated lab environment with virtually no background noise, a 1 dB change yields the smallest perceptible difference in loudness. However, in average real-world listening conditions, most people can’t notice a loudness change less than 3 dB. A 10 dB change results in about a doubling of perceived loudness. It doesn’t matter if you’re going from 60 to 70 dBSPL or from 80 to 90 dBSPL. The increase still sounds approximately like a doubling of loudness. In contrast, going from 60 to 70 dBSPL is an increase of 43.24 mPa, while going from 80 to 90 dBSPL is an increase of 432.5 mPa. Here you can see that saying that you “turned up the volume” by a certain air pressure amplitude wouldn’t give much information about how much louder it’s going to sound. Talking about loudness-changes in terms of decibels communicates more.
[table caption=”Table 4.2 How sound level changes in dB are perceived”]
Change of sound amplitude,How it is perceived in human hearing
1 dB,”smallest perceptible difference in loudness, only perceptible in acoustically-insulated noiseless environments”
3 dB,smallest perceptible change in loudness for most people in real-world environments
+10 dB,an approximate doubling of loudness
-10 dB change,an approximate halving of loudness
[/table]
You may have noticed that when we talk about a “decibel change,” we refer to it as simply decibels or dB, whereas if we are referring to a sound loudness level relative to the threshold of hearing, we refer to it as dBSPL. This is correct usage. The difference between 90 and 80 dBSPL is 10 dB. The difference between any two decibels levels that have the same reference point is always measured in dimensionless dB. We’ll return to this in a moment when we try some practice problems in Section 2.
4.1.5.2 Various Usages of Decibels
Now let’s look at the origin of the definition of decibel and how the word can be used in a variety of contexts.
The bel, named for Alexander Graham Bell, was originally defined as a unit for measuring power. For clarity, we’ll call this the power difference bel, also denoted :
[equation caption=”Equation 4.5 , power difference bel”]
$$!1\: power\: difference\: bel=\Delta Power\: B=\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
[/equation]
The decibel is 1/10 of a bel. The decibel turns out to be a more useful unit than the bel because it provides better resolution. A bel doesn’t break measurements into small enough units for most purposes.
We can derive the power difference decibel (Δ Power dB) from the power difference bel simply by multiplying the log by 10. Another name for ΔPower dB is dBPWL (decibels-power-level).
[equation caption=”Equation 4.6, abbreviated dBPWL”]
$$!\Delta Power\: B=dBPWL=10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
[/equation]
When this definition is applied to give a sense of the acoustic power of a sound, then is the power of sound at the threshold of hearing, which is $$10^{-12}W=1pW$$ (picowatt).
Sound can also be measured in terms of intensity. Since intensity is defined as power per unit area, the units in the numerator and denominator of the decibel ratio are $$\frac{W}{m^{2}}$$, and the threshold of hearing intensity is $$10^{-12}\frac{W}{m^{2}}$$. This gives us the following definition of ΔIntensity dB, also commonly referred to as dBSIL (decibels-sound intensity level).
[equation caption=”Equation 4.7 , abbreviated dBSIL”]
$$!\Delta Intensity\, dB=dBSIL=10\log_{10}\left ( \frac{I_{1}}{I_{0}} \right )$$
[/equation]
Neither power nor intensity is a convenient way of measuring the loudness of sound. We give the definitions above primarily because they help to show how the definition of dBSPL was derived historically. The easiest way to measure sound loudness is by means of air pressure amplitude. When sound is transmitted, air pressure changes are detected by a microphone and converted to voltages. If we consider the relationship between voltage and power, we can see how the definition of ΔVoltage dB was derived from the definition of ΔPower dB. By Equation 4.3, we know that power varies with the square of voltage. From this we get: $$!10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )=10\log_{10}\left ( \left ( \frac{V_{1}}{V_{0}} \right )^{2} \right )=20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$ The relationship between power and voltage explains why there is a factor of 20 is in Equation 4.4.
[aside width=”125px”]
$$\log_{b}\left ( y^{x} \right )=x\log_{b}y$$
[/aside]
We can show how Equation 4.4 is applied to convert from air pressure amplitude to dBSPL and vice versa. Let’s say we begin with the air pressure amplitude of a humming refrigerator, which is about 0.002 Pa.
$$!dBSPL=20\log_{10}\left ( \frac{0.002\: Pa}{0.00002\: Pa} \right )=20\log_{10}\left ( 100 \right )=20\ast 2=40\: dBSPL$$
Working in the opposite direction, you can convert the decibel level of normal conversation (60 dBSPL) to air pressure amplitude:
$$\begin{align*}& 60=20\log_{10}\left ( \frac{0.002\: Pa}{0.00002\: Pa} \right )=20\log_{10}\left ( 50000x/Pa \right ) \\&\frac{60}{20}=\log_{10}\left ( 50000x/Pa \right ) \\&3=\log_{10}\left ( 50000x/Pa \right ) \\ &10^{3}= 50000x/Pa\\&x=\frac{1000}{50000}Pa \\ &x=0.02\: Pa \end{align*}$$
[aside width=”125px”]
If $$x=\log_{b}y$$
then $$b^{x}=y$$
[/aside]
Thus, 60 dBSPL corresponds to air pressure amplitude of 0.02 Pa.
Rarely would you be called upon to do these conversions yourself. You’ll almost always work with sound intensity as decibels. But now you know the mathematics on which the dBSPL definition is based.
So when would you use these different applications of decibels? Most commonly you use dBSPL to indicate how loud things seem relative to the threshold of hearing. In fact, you use this type of decibel so commonly that the SPL is often dropped off and simply dB is used where the context is clear. You learn that human speech is about 60 dB, rock music is about 110 dB, and the loudest thing you can listen to without hearing damage is about 120 dB – all of these measurements implicitly being dBSPL.
The definition of intensity decibels, dBSIL, is mostly of interest to help us understand how the definition of dBSPL can be derived from dBPWL. We’ll also use the definition of intensity decibels in an explanation of the inverse square law, a rule of thumb that helps us predict how sound loudness decreases as sound travels through space in a free field (Section 4.2.1.6).
There’s another commonly-used type of decibel that you’ll encounter in digital audio software environments – the decibel-full-scale (dBFS). You may not understand this type of decibel completely until you’ve read Chapter 5 because it’s based on how audio signals are digitized at a certain bit depth (the number of bits used for each audio sample). We’ll give the definition here for completeness and revisit it in Chapter 5. The definition of dBFS uses the largest-magnitude sample size for a given bit depth as its reference point. For a bit depth of n, this largest magnitude would be $$2^{n-1}$$.
[equation caption=”Equation 4.8 Decibels-full-scale, abbreviated dBFS”]
$$!dBFS = 20\log_{10}\left ( \frac{\left | x \right |}{2^{n-1}} \right )$$
where n is a given bit depth and x is an integer sample value between $$-2^{n-1}$$ and $$2^{n-1}-1$$.
[/equation]
Figure 4.2 shows an audio processing environment where a sound wave is measured in dBFS. Notice that since $$\left | x \right |$$ is never more than $$2^{n-1}$$, $$log_{10}\left ( \frac{\left | x \right |}{2^{n-1}} \right )$$ is never a positive number. When you first use dBFS it may seem strange because all sound levels are at most 0. With dBFS, 0 represents maximum amplitude for the system, and values move toward -∞ as you move toward the horizontal axis, i.e., toward quieter sounds.
The discussion above has considered decibels primarily as they measure sound loudness. Decibels can also be used to measure relative electrical power or voltage. For example, dBV measures voltage using 1 V as a reference level, dBu measures voltage using 0.775 V as a reference level, and dBm measures power using 0.001 W as a reference level. These applications come into play when you’re considering loudspeaker or amplifier power, or wireless transmission signals. In Section 2, we’ll give you some practical applications and problems where these different types of decibels come into play.
The reference levels for different types of decibels are listed in Table 4.3. Notice that decibels are used in reference to the power of loudspeakers or the input voltage to audio devices. We’ll look at these applications more closely in Section 2. Of course, there are many other common usages of decibels outside of the realm of sound.
[table caption=”Table 4.3 Usages of the term decibels with different reference points” width=”80%”]
what is being measured,abbreviations in common usage,common reference point,equation for conversion to decibels
Acoustical,,,
sound power ,dBPWL or ΔPower dB,$$P_{0}=10^{-12}W=1pW(picowatt)$$ ,$$10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
sound intensity ,dBSIL or ΔIntensity dB,”threshold of hearing, $$I_{0}=10^{-12}\frac{W}{m^{2}}”$$,$$10\log_{10}\left ( \frac{I_{1}}{i_{0}} \right )$$
sound air pressure amplitude ,dBSPL or ΔVoltage dB,”threshold of hearing, $$P_{0}=0.00002\frac{N}{m^{2}}=2\ast 10^{-5}Pa$$”, $$20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$
sound amplitude,dBFS, “$$2^{n-1}$$ where n is a given bit depth x is a sample value, $$-2^{n-1} \leq x \leq 2^{n-1}-1$$”,dBFS=$$20\log_{10}\left ( \frac{\left | x \right |}{2^{n-1}} \right )$$
Electrical,,,
radio frequency transmission power,dBm,$$P_{0}=1 mW = 10^{-3} W$$ ,$$10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
loudspeaker acoustical power,dBW,$$P_{0}=1 W$$,$$10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
input voltage from microphone; loudspeaker voltage; consumer level audio voltage,dBV,$$V_{0}=1 V$$,$$20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$
professional level audio voltage,dBu,$$V_{0}=0.775 V$$,$$20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$
[/table]
4.1.5.3 Peak Amplitude vs. RMS Amplitude
Microphones and sound level meters measure the amplitude of sound waves over time. There are situations in which you may want to know the largest amplitude over a time period. This “largest” can be measured in one of two ways: as peak amplitude or as RMS amplitude.
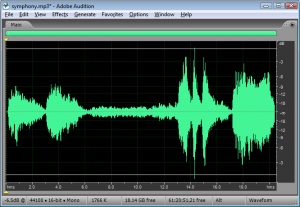
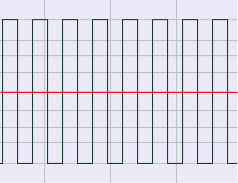
Let’s assume that the microphone or sound level meter is measuring sound amplitude. The sound pressure level of greatest magnitude over a given time period is called the peak amplitude. For a single-frequency sound representable by a sine wave, this would be the level at the peak of the sine wave. The sound represented by Figure 4.3 would obviously be perceived as louder than the same-frequency sound represented by Figure 4.4. However, how would the loudness of a sine-wave-shaped sound compare to the loudness of a square-wave-shaped sound with the same peak amplitude (Figure 4.3 vs. Figure 4.5)? The square wave would actually sound louder. This is because the square wave is at its peak level more of the time as compared to the sine wave. To account for this difference in perceived loudness, RMS amplitude (root-mean-square amplitude) can be used as an alternative to peak amplitude, providing a better match for the way we perceive the loudness of the sound.


Rather than being an instantaneous peak level, RMS amplitude is similar to a standard deviation, a kind of average of the deviation from 0 over time. RMS amplitude is defined as follows:
[equation caption=”Equation 4.9 Equation for RMS amplitude, $$V_{RMS}$$”]
$$!V_{RMS}=\sqrt{\frac{\sum _{i=1}^{n}\left ( S_{i} \right )^{2}}{n}}$$
where n is the number of samples taken and $$S_{i}$$ is the $$i^{th}$$ sample.
[/equation]
[aside]In some sources, the term RMS power is used interchangeably with RMS amplitude or RMS voltage. This isn’t very good usage. To be consistent with the definition of power, RMS power ought to mean “RMS voltage multiplied by RMS current.” Nevertheless, you sometimes see term RMS power used as a synonym of RMS amplitude as defined in Equation 4.9.[/aside]
Notice that squaring each sample makes all the values in the summation positive. If this were not the case, the summation would be 0 (assuming an equal number of positive and negative crests) since the sine wave is perfectly symmetrical.
The definition in Equation 4.9 could be applied using whatever units are appropriate for the context. If the samples are being measured as voltages, then RMS amplitude is also called RMS voltage. The samples could also be quantized as values in the range determined by the bit depth, or the samples could also be measured in dimensionless decibels, as shown for Adobe Audition in Figure 4.6.
For a pure sine wave, there is a simple relationship between RMS amplitude and peak amplitude.
[equation caption=”Equation 4.10 Relationship between $$V_{rms}$$ and $$V_{peak}$$ for pure sine waves”]
for pure sine waves
$$!V_{RMS}=\frac{V_{peak}}{\sqrt{2}}=0.707\ast V_{peak}$$
and
$$!V_{peak}=1.414\ast V_{RMS}$$
[/equation]
Of course most of the sounds we hear are not simple waveforms like those shown; natural and musical sounds contain many frequency components that vary over time. In any case, the RMS amplitude is a better model for our perception of the loudness of complex sounds than is peak amplitude.
Sound processing programs often give amplitude statistics as either peak or RMS amplitude or both. Notice that RMS amplitude has to be defined over a particular window of samples, labeled as Window Width in Figure 4.6. This is because the sound wave changes over time. In the figure, the window width is 1000 ms.

You need to be careful will some usages of the term “peak amplitude.” For example, VU meters, which measure signal levels in audio equipment, use the word “peak” in their displays, where RMS amplitude would be more accurate. Knowing this is important when you’re setting levels for a live performance, as the actual peak amplitude is higher than RMS. Transients like sudden percussive noises should be kept well below what is marked as “peak” on a VU meter. If you allow the level to go too high, the signal will be clipped.