5.1.1 Analog Vs. Digital
Today’s world of sound processing is quite different from what it was just a few decades ago. A large portion of sound processing is now done by digital devices and software – mixers, dynamics processors, equalizers, and a whole host of tools that previously existed only as analog hardware. This is not to say, however, that in all stages – from capturing to playing – sound is now treated digitally. As it is captured, processed, and played back, an audio signal can be transformed numerous times from analog-to-digital or digital-to-analog. A typical scenario for live sound reinforcement is pictured in Figure 5.1. In this setup, a microphone – an analog device – detects continuously changing air pressure, records this as analog voltage, and sends the information down a wire to a digital mixing console. Although the mixing console is a digital device, the first circuit within the console that the audio signal encounters is an analog preamplifier. The preamplifier amplifies the voltage of the audio signal from the microphone before passing it on to an analog-to-digital converter (ADC). The ADC performs a process called digitization and then passes the signal into one of many digital audio streams in the mixing console. The mixing console applies signal-specific processing such as equalization and reverberation, and then it mixes and routes the signal together with other incoming signals to an output connector. Usually this output is analog, so the signal passes through a digital-to-analog converter (DAC) before being sent out. That signal might then be sent to a digital system processor responsible for applying frequency, delay, and dynamics processing for the entire sound system and distributing that signal to several outputs. The signal is similarly converted to digital on the way into this processor via an ADC, and then back through a DAC to analog on the way out. The analog signals are then sent to analog power amplifiers before they are sent to a loudspeaker, which converts the audio signal back into a sound wave in the air.
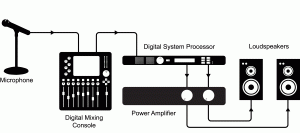
A sound system like the one pictured can be a mix of analog and digital devices, and it is not always safe to assume a particular piece of gear can, will, or should be one type or the other. Even some power amplifiers nowadays have a digital signal stage that may require conversion from an analog input signal. Of course, with the prevalence of digital equipment and computerized systems, it is likely that an audio signal will exist digitally at some point in its lifetime. In systems using multiple digital devices, there are also ways of interfacing two pieces of equipment using digital signal connections that can maintain the audio in its digital form and eliminate unnecessary analog-to-digital and digital-to-analog conversions. Specific types of digital signal connections and related issues in connecting digital devices are discussed later in this chapter.
The previous figure shows a live sound system setup. A typical setup of a computer-based audio recording and editing system is pictured in Figure 5.2. While this workstation is essentially digital, the DAW, like the live sound system, includes analog components such as microphones and loudspeakers.
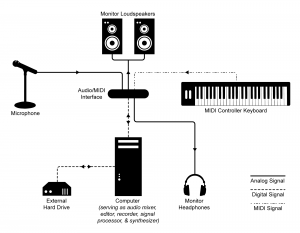
Understanding the digitization process paves the way for understanding the many ways that digitized sound can be manipulated. Let’s look at this more closely.
5.1.2 Digitization
5.1.2.1 Two Steps: Sampling and Quantization
In the realm of sound, the digitization process takes an analog occurrence of sound, records it as a sequence of discrete events, and encodes it in the binary language of computers. Digitization involves two main steps, sampling and quantization.
Sampling is a matter of measuring air pressure amplitude at equally-spaced moments in time, where each measurement constitutes a sample. The number of samples taken per second (samples/s) is the sampling rate. Units of samples/s are also referred to as Hertz (Hz). (Recall that Hertz is also used to mean cycles/s with regard to a frequency component of sound. Hertz is an overloaded term, having different meanings depending on where it is used, but the context makes the meaning clear.)
[aside]It’s possible to use real numbers instead of integers to represent sample values in the computer, but that doesn’t get rid of the basic problem of quantization. Although a wide range of samples values can be represented with real numbers, there is still only a finite number of them, so rounding is still be necessary with real numbers.[/aside]
Quantization is a matter of representing the amplitude of individual samples as integers expressed in binary. The fact that integers are used forces the samples to be measured in a finite number of discrete levels. The range of the integers possible is determined by the bit depth, the number of bits used per sample. A sample’s amplitude must be rounded to the nearest of the allowable discrete levels, which introduces error in the digitization process.
When sound is recorded in digital format, a sampling rate and a bit depth are specified. Often there are default audio settings in your computing environment, or you may be prompted for initial settings, as shown in Figure 5.3. The number of channels must also be specified – mono for one channel and stereo for two. (More channels are possible in the final production, e.g., 5.1 surround.)
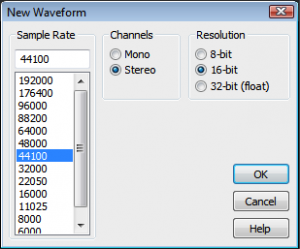
A common default setting is designated CD quality audio, with a sampling rate of 44,100 Hz, a bit depth of 16 bits (i.e., two bytes) per channel, with two channels. Sampling rate and bit depth has an impact on the quality of a recording. To understand how this works, let’s look at sampling and quantization more closely.
5.1.2.2 Sampling and Aliasing
[wpfilebase tag=file id=116 tpl=supplement /]
Recall from Chapter 2 that the continuously changing air pressure of a single-frequency sound can be represented by a sine function, as shown in Figure 5.4. One cycle of the sine wave represents one cycle of compression and rarefaction of the sound wave. In digitization, a microphone detects changes in air pressure, sends corresponding voltage changes down a wire to an ADC, and the ADC regularly samples the values. The physical process of measuring the changing air pressure amplitude over time can be modeled by the mathematical process of evaluating a sine function at particular points across the horizontal axis.
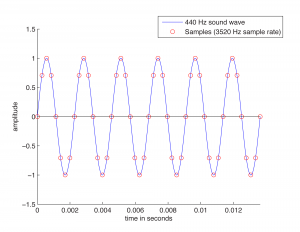
Figure 5.4 shows eight samples being taken for each cycle of the sound wave. The samples are represented as circles along the waveform. The sound wave has a frequency of 440 cycles/s (440 Hz), and the sampling rate has a frequency of 3520 samples/s (3520 Hz). The samples are stored as binary numbers. From these stored values, the amplitude of the digitized sound can be recreated and turned into analog voltage changes by the DAC.
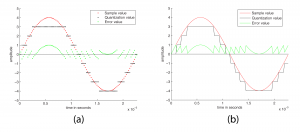
The quantity of these stored values that exists within a given amount of time, as defined by the sampling rate, is important to capturing and recreating the frequency content of the audio signal. The higher the frequency content of the audio signal, the more samples per second (higher sampling rate) are needed to accurately represent it in the digital domain. Consider what would happen if only one sample was taken for every one-and-a-quarter cycles of the sound wave, as pictured in Figure 5.5. This would not be enough information for the DAC to correctly reconstruct the sound wave. Some cycles have been “jumped over” by the sampling process. In the figure, the higher-frequency wave is the original analog 440 Hz wave.
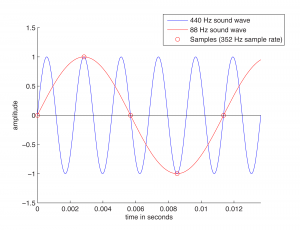
When the sampling rate is too low, the reconstructed sound wave appears to be lower-frequency than the original sound (or have an incorrect frequency component, in the case of a complex sound wave). This is a phenomenon called aliasing – the incorrect digitization of a sound frequency component resulting from an insufficient sampling rate.
For a single-frequency sound wave to be correctly digitized, the sampling rate must be at least twice the frequency of the sound wave. More generally, for a sound with multiple frequency components, the sampling rate must be at least twice the frequency of the highest frequency component. This is known as the Nyquist theorem.
[equation]
The Nyquist Theorem
Given a sound with maximum frequency component of f Hz, a sampling rate of at least 2f is required to avoid aliasing. The minimum acceptable sampling rate (2f in this context) is called the Nyquist rate.
Given a sampling rate of f, the highest-frequency sound component that can be correctly sampled is f/2. The highest frequency component that can be correctly sampled is called the Nyquist frequency.
[/equation]
In practice, aliasing is generally not a problem. Standard sampling rates in digital audio recording environments are high enough to capture all frequencies in the human-audible range. The highest audible frequency is about 20,000 Hz. In fact, most people don’t hear frequencies this high, as our ability to hear high frequencies diminishes with age. CD quality sampling rate is 44,100 Hz (44.1 kHz), which is acceptable as it is more than twice the highest audible component. In other words, with CD quality audio, the highest frequency we care about capturing (20 kHz for audibility purposes) is less than the Nyquist frequency for that sampling rate, so this is fine. A sampling rate of 48 kHz is also widely supported, and sampling rates go up as high as 192 kHz.
Even if a sound contains frequency components that are above the Nyquist frequency, to avoid aliasing the ADC generally filters them out before digitization.
Section 5.3.1 gives more detail about the mathematics of aliasing and an algorithm for determining the frequency of the aliased wave in cases where aliasing occurs.
5.1.2.3 Bit Depth and Quantization Error
When samples are taken, the amplitude at that moment in time must be converted to integers in binary representation. The number of bits used for each sample, called the bit depth, determines the precision with which you can represent the sample amplitudes. For this discussion, we assume that you know that basics of binary representation, but let’s review briefly.
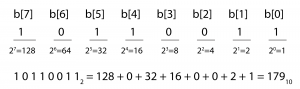
Binary representation, the fundamental language of computers, is a base 2 number system. Each bit in a binary number holds either a 1 or a 0. Eight bits together constitute one byte. The bit positions in a binary number are numbered from right to left starting at 0, as shown in Figure 5.6. The rightmost bit is called the least significant bit, and the leftmost is called the most significant bit. The ith bit is called b[i] .
The value of an n-bit binary number is equal to
[equation caption=”Equation 5.1″]
$$!\sum_{t=0}^{n-1}b\left [ i \right ]\ast 2^{i}$$
[/equation]
Notice that doing the summation from causes the terms in the sum to be in the reverse order from that shown in Figure 5.6. The summation for our example is
$$!10110011_{2}=1\ast 1+1\ast 2+0\ast 4+0\ast 8+1\ast 16+1\ast 32+0\ast 64+1\ast 128=179_{10}$$
Thus, 10110011 in base 2 is equal to 179 in base 10. (Base 10 is also called decimal.) We leave off the subscript 2 in binary numbers and the subscript 10 in decimal numbers when the base is clear from the context.
From the definition of binary numbers, it can be seen that the largest decimal number that can be represented with an n-bit binary number is $$2^{n}-1$$, and the number of different values that can be represented is $$2^{n}$$. For example, the decimal values that can be represented with an 8-bit binary number range from 0 to 255, so there are 256 different values.
These observations have significance with regard to the bit depth of a digital audio recording. A bit depth of 8 allows 256 different discrete levels at which samples can be recorded. A bit depth of 16 allows 216 = 65,536 discrete levels, which in turn provides much higher precision than a bit depth of 8.
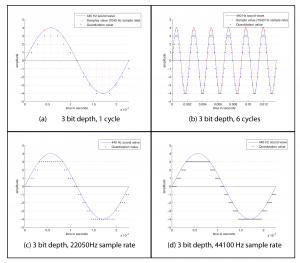
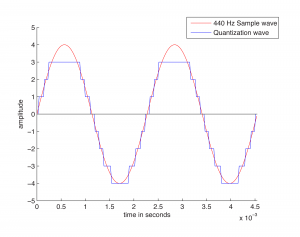
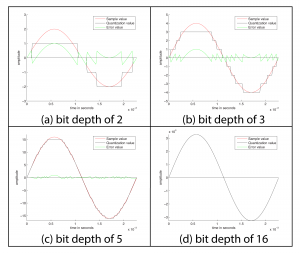
The process of quantization is illustrated Figure 5.7. Again, we model a single-frequency sound wave as a sine function, centering the sine wave on the horizontal axis. We use a bit depth of 3 to simplify the example, although this is far lower than any bit depth that would be used in practice. With a bit depth of 3, 23 = 8 quantization levels are possible. By convention, half of the quantization levels are below the horizontal axis (that is, $$2^{n-1}$$ of the quantization levels). One level is the horizontal axis itself (level 0), and $$2^{n-1}-1$$ levels are above the horizontal axis. These levels are labeled in the figure, ranging from -4 to 3. When a sound is sampled, each sample must be scaled to one of $$2^{n}$$ discrete levels. However, the samples in reality might not fall neatly onto these levels. They have to be rounded up or down by some consistent convention. We round to the nearest integer, with the exception that values at 3.5 and above are rounded down to 3. The original sample values are represented by red dots on the graphs. The quantized values are represented as black dots. The difference between the original samples and the quantized samples constitutes rounding error. The lower the bit depth, the more values potentially must be rounded, resulting in greater quantization error. Figure 5.8 shows a simple view of the original wave vs. the quantized wave.
[wpfilebase tag=file id=117 tpl=supplement /]
Quantization error is sometimes referred to as noise. Noise can be broadly defined as part of an audio signal that isn’t supposed to be there. However, some sources would argue that a better term for quantization error is distortion, defining distortion as an unwanted part of an audio signal that is related to the true signal. If you subtract the stair-step wave from the true sine wave in Figure 5.8, you get the green part of the graphs in Figure 5.9. This is precisely the error – i.e., the distortion – resulting from quantization. Notice that the error follows a regular pattern that changes in tandem with the original “correct” sound wave. This makes the distortion sound more noticeable in human perception, as opposed to completely random noise. The error wave constitutes sound itself. If you take the sample values that create the error wave graph in Figure 5.9, you can actually play them as sound. You can compare and listen to the effects of various bit depths and the resulting quantization error in the Max Demo “Bit Depth” linked to this section.
For those who prefer to distinguish between noise and distortion, noise is defined as an unwanted part of an audible signal arising from environmental interference – like background noise in a room where a recording is being made, or noise from the transmission of an audio signal along wires. This type of noise is more random than the distortion caused by quantization error. Section 3 shows you how you can experiment with sampling and quantization in MATLAB, C++, and Java programming to understand the concepts in more detail.
5.1.2.4 Dynamic Range
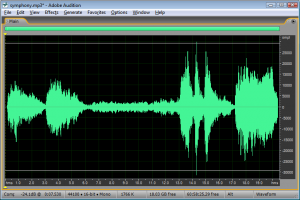
Another way to view the implications of bit depth and quantization error is in terms of dynamic range. The term dynamic range has two main usages with regard to sound. First, an occurrence of sound that takes place over time has a dynamic range, defined as the range between the highest and lowest amplitude moments of the sound. This is best illustrated by music. Classical symphonic music generally has a wide dynamic range. For example, “Beethoven’s Fifth Symphony” begins with a high amplitude “Bump bump bump baaaaaaaa” and continues with a low-amplitude string section. The difference between the loud and quiet parts is intentionally dramatic and is what gives the piece a wide dynamic range. You can see this in the short clip of the symphony graphed in Figure 5.10. The dynamic range of this clip is a function of the ratio between the largest sample value and the magnitude of the smallest. Notice that you don’t measure the range across the horizontal access but from the highest-magnitude sample either above or below the axis to the lowest-magnitude sample on the same side of the axis. A sound clip with a narrow dynamic range has a much smaller difference between the loud and quiet parts. In this usage of the term dynamic range, we’re focusing on the dynamic range of a particular occurrence of sound or music.
[aside]
MATLAB Code for Figure 5.11 and Figure 5.12:
hold on;
f = 440;T = 1/f;
Bdepth = 3; bit depth
Drange = 2^(Bdepth-1); dynamic range
axis = [0 2*T -(Drange+1) Drange+1];
SRate = 44100; %sample rate
sample_x = (0:2*T*SRate)./SRate;
sample_y = Drange*sin(2*pi*f*sample_x);
plot(sample_x,sample_y,'r-');
q_y = round(sample_y); %quantization value
for i = 1:length(q_y)
if q_y(i) == Drange
q_y(i) = Drange-1;
end
end
plot(sample_x,q_y,'-')
for i = -Drange:Drange-1 %quantization level
y = num2str(i); fplot(y,axis,'k:')
end
legend('Sample wave','Quantization wave','Quantization level')
y = '0'; fplot(y,axis,'k-')
ylabel('amplitude');xlabel('time in seconds');
hold off;
[/aside]
In another usage of the term, the potential dynamic range of a digital recording refers to the possible range of high and low amplitude samples as a function of the bit depth. Choosing the bit depth for a digital recording automatically constrains the dynamic range, a higher bit depth allowing for a wider dynamic range.
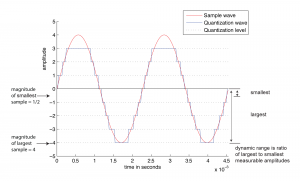
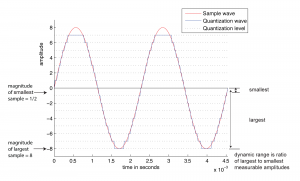
Consider how this works. A digital recording environment has a maximum amplitude level that it can record. On the scale of n-bit samples, the maximum amplitude (in magnitude) would be $$2_{n-1}$$. The question is this: How far, relatively, can the audio signal fall below the maximum level before it is rounded down to silence? The figures below show the dynamic range at a bit depth of 3 (Figure 5.11) compared to the dynamic range at a bit depth of 4 (Figure 5.12). Again, these are non-practical bit depths chosen for simplicity of illustration. The higher bit depth gives a wider range of sound amplitudes that can be recorded. The smaller bit depth loses more of the quiet sounds when they are rounded down to zero or overpowered by the quantization noise. You can see this in the right hand view of Figure 5.13, where a portion of “Beethoven’s Ninth Symphony” has been reduced to four bits per sample.
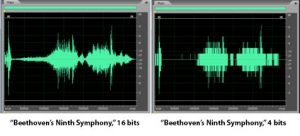
[wpfilebase tag=file id=40 tpl=supplement /]
The term dynamic range has a precise mathematical definition that relates back to quantization error. In the context of music, we encountered dynamic range as a ratio between the loudest and quietest musical passages of a song or performance. Digitally, the loudest potential passage of the music (or other audio signal) that could be represented would have full amplitude (all bits on). The quietest possible passage is the quantization noise itself. Any sound quieter than that would simply be masked by the noise or rounded down to silence. The ratio between the loudest and quietest parts is therefore the highest (possible) amplitude of the audio signal compared to the amplitude of the quantization noise, or the ratio between the signal level to the noise level. This is what is known as signal-to-quantization-noise-ratio (SQNR), and in this context, dynamic range is the same thing. This definition is given in Equation 5.2.
[equation caption=”Equation 5.2″]
Given a bit depth of n, the dynamic range of a digital audio recording is equal to
$$!20\log_{10}\left ( \frac{2^{n-1}}{1/2} \right )dB$$
[/equation]
You can see from the equation that dynamic range as SQNR is measured in decibels. Decibels are a dimensionless unit derived from the logarithm of the ratio between two values. For sound, decibels are based on the ratio between the air pressure amplitude of a given sound and the air pressure amplitude of the threshold of hearing. For dynamic range, decibels are derived from the ratio between the maximum and minimum amplitudes of an analog waveform quantized with n bits. The maximum magnitude amplitude is $$2^{n-1}$$. The minimum amplitude of an analog wave that would be converted to a non-zero value when it is quantized is ½. Signal-to-quantization-noise is based on the ratio between these maximum and minimum values for a given bit depth. It turns out that this is exactly the same value as the dynamic range.
Equation 5.2 can be simplified as shown in Equation 5.3.
[equation caption=”Equation 5.3″]
$$!20\log_{10}\left ( \frac{2^{n-1}}{1/2} \right )=20\log_{10}\left ( 2^{n} \right )=20n\log_{10}\left ( 2 \right )\approx 6.04n$$
[/equation]
[wpfilebase tag=file id=118 tpl=supplement /]
Equation 5.3 gives us a method for determining the possible dynamic range of a digital recording as a function of the bit depth. For bit depth n, the possible dynamic range is approximately 6n dB. A bit depth of 8 gives a dynamic range of approximately 48 dB, a bit depth of 16 gives a dynamic range of about 96 dB, and so forth.
When we introduced this section, we added the adjective “potential” to “dynamic range” to emphasize that it is the maximum possible range that can be used as a function of the bit depth. But not all of this dynamic range is used if the amplitude of a digital recording is relatively low, never reaching its maximum. Thus, we it is important to consider the actual dynamic range (or actual SQNR) as opposed to the potential dynamic range (or potential SQNR, just defined). Take, for example, the situation illustrated in Figure 5.15. A bit depth of 7 has been chosen. The amplitude of the wave is 24 dB below the maximum possible. Because the sound uses so little of its potential dynamic range, the actual dynamic range is small. We’ve used just a simple sine wave in this example so that you can easily see the error wave in proportion to the sine wave, but you can imagine a music recording that has a low actual dynamic range because the recording was done at a low level of amplitude. The difference between potential dynamic range and actual dynamic range is illustrated in detail in the interactive Max demo associated with this section. This demo shows that, in addition to choosing a bit depth appropriately to provide sufficient dynamic range for a sound recording, it’s important that you use the available dynamic range optimally. This entails setting microphone input voltage levels so that the loudest sound produced is as close as possible to the maximum recordable level. These practical considerations are discussed further in Section 5.2.2.
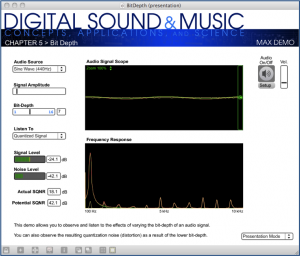
We have one more related usage of decibels to define in this section. In the interface of many software digital audio recording environments, you’ll find that decibels-full-scale (dBFS) is used. (In fact, it is used in the Signal and Noise Level meters in Figure 5.15.) As you can see in Figure 5.16, which shows amplitude in dBFS, the maximum amplitude is 0 dBFS, at equidistant positions above and below the horizontal axis. As you move toward the horizontal axis (from either above or below) through decreasing amplitudes, the dBFS values become increasingly negative.
The equation for converting between dB and dBFS is given in Equation 5.4
[equation caption=”Equation 5.4″]
For n-bit samples, decibels-full-scale (dBFS) is defined as follows:
$$!dBFS=20\log_{10}\left ( \frac{x}{2^{n-1}} \right )$$
where $$x$$ is an integer sample value between 0 and $$2^{n-1}$$.
[/equation]
Generally, computer-based sample editors allow you to select how you want the vertical axis labeled, with choices including sample values, percentage, values normalized between -1 and 1, and dBFS.
Chapter 7 goes into more depth about dynamics processing, the adjustment of dynamic range of an already-digitized sound clip.
5.1.2.5 Audio Dithering and Noise Shaping
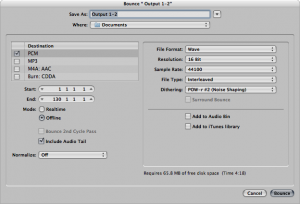
It’s possible to take an already-recorded audio file and reduce its bit depth. In fact, this is commonly done. Many audio engineers keep their audio files at 24 bits while they’re working on them, and reduce the bit depth to 16 bits when they’re finished processing the files or ready to burn to an audio CD. The advantage of this method is that when the bit depth is higher, less error is introduced by processing steps like normalization or adjustment of dynamics. Because of this advantage, even if you choose a bit depth of 16 from the start, your audio processing system may be using 24 bits (or an even higher bit depth) behind the scenes anyway during processing, as is the case with Pro Tools.
Audio dithering is a method to reduce the quantization error introduced by a low bit depth. Audio dithering can be used by an ADC when quantization is initially done, or it can be used on an already-quantized audio file when bit depth is being reduced. Oddly enough, dithering works by adding a small amount of random noise to each sample. You can understand the advantage of doing this if you consider a situation where a number of consecutive samples would all round down to 0 (i.e., silence), causing breaks in the sound. If a small random amount is added to each of these samples, some round up instead of down, smoothing over those breaks. In general, dithering reduces the perceptibility of the distortion because it causes the distortion to no longer follow exactly in tandem with the pattern of the true signal. In this situation, low-amplitude noise is a good trade-off for distortion.
Noise shaping is a method that can be used in conjunction with audio dithering to further compensate for bit-depth reduction. It works by raising the frequency range of the rounding error after dithering, putting it into a range where human hearing is less sensitive. When you reduce the bit depth of an audio file in an audio processing environment, you are often given an option of applying dithering and noise shaping, as shown in Figure 5.17 Dithering can be done without noise shaping, but noise shaping is applied only after dithering. Also note that dithering and noise shaping cannot be done apart from the requantization step because they are embedded into the way the requantization is done. A popular algorithm for dithering and noise shaping is the proprietary POW-r (Psychoacoustically Optimized Wordlength Reduction), which is built into Pro Tools, Logic Pro, Sonar, and Ableton Live.
Dithering and noise shaping are discussed in more detail in Section 5.3.7.
5.1.3 Audio Data Streams and Transmission Protocols
Audio data passed from one device to another is referred to as a stream. There are several different formats for transmitting a digital audio stream between devices. In some cases, you might want to interconnect two pieces of equipment digitally, but they don’t offer a compatible transmission protocol. The best thing to do is make sure you purchase equipment that is compatible with the equipment you already have. In order to succeed at this, you’ll need to understand and be able to identify the various options for digital audio transmission.
The most common transmission protocol, particularly in consumer-grade equipment is the Sony/Phillips Digital Interconnect Format (S/PDIF). With S/PDIF you can transmit two channels on a single wire. Typically this means you can transmit both the left and right channels of a stereo pair using a single cable instead of two cables required for analog transmission. S/PDIF can be transmitted electrically or optically. Electrical transmission involves RCA (Radio Corporation of America) connectors and a low loss, high bandwidth coaxial cable. This cable is different from the cable you would use for analog transmission. For S/PDIF you need a cable like what is used for video. S/PDIF transmits the digital data electrically in a stream of square wave pulses. Using cheap, low bandwidth cable can result in a loss of high frequency content that can ultimately lose the square wave form, resulting in data loss. When looking for a cable for electrical S/PDIF transmission, look for something with RCA connectors on each end and an impedance of 75 W.
S/PDIF can also be transmitted optically using an optical cable with TOSLINK (TOShiba-LINK) connectors. Optical transmission has the advantage of being able to run longer distances without the risk of signal loss, and it is not susceptible to electromagnetic interference like an electrical signal. Optical cables are more easily broken so if you plan to move your equipment around, you should invest in an optical cable that has good insulation.

S/PDIF is considered a consumer grade transmission protocol. S/PDIF has a professional grade cousin called AES3, more commonly known as AES/EBU (Audio Engineering Society/European Broadcasting Union). The actual format of the digital stream is almost identical. The main differences are the type of cable and connectors used and the maximum distance you can reliably transmit the signal. AES/EBU can be run electrically as a balanced signal using three pin XLR connectors with a 110 W twisted pair cable or unbalanced using BNC connectors a with a 75 W coaxial cable. The unbalanced version has a maximum transmission distance of 1000 meters as opposed to the 100 meters maximum for the balanced version. The balanced signal is by far the most common implementation as shown in Figure 5.19.

If you need to transmit more than two channels of digital audio between devices, there are several options available. The most common is the ADAT Optical Interface (Alesis Digital Audio Tape). Alesis developed the system to allow signal transfer between their eight-track digital audio tape recorders, but the system has since been widely adopted for multi-channel digital signal transmission between devices at short distances. ADAT can transmit eight channels of audio at sampling rates up to 48 kHz or four channels at sampling rates up to 96 kHz. ADAT uses the same optical TOSLINK cable used for S/PDIF. This makes it relatively inexpensive for the consumer. However, the protocol must be licensed from Alesis if a manufacturer wants to implement it in their equipment.
There are several other emerging standards for multi-channel digital audio transmission, more than we can cover in the scope of this chapter. What is important to know is that most protocols allow digital transmission of 64 channels or more of digital audio over long distances using fiber optic, or CAT-5e cable. Examples of this kind of transmission include MADI, AVB, CobraNet, A-Net, and mLAN. If you need this level of functionality, you will likely be able to purchase interface cards that use these protocols for most computers and digital mixing consoles.
5.1.4 Signal Path in an Audio Recording System
In Section 5.1.1, we illustrated a typical setup for a computer-based digital audio recording and editing system. Let’s look at this more closely now, with special attention to the signal path and conversions of the audio stream between analog and digital forms.
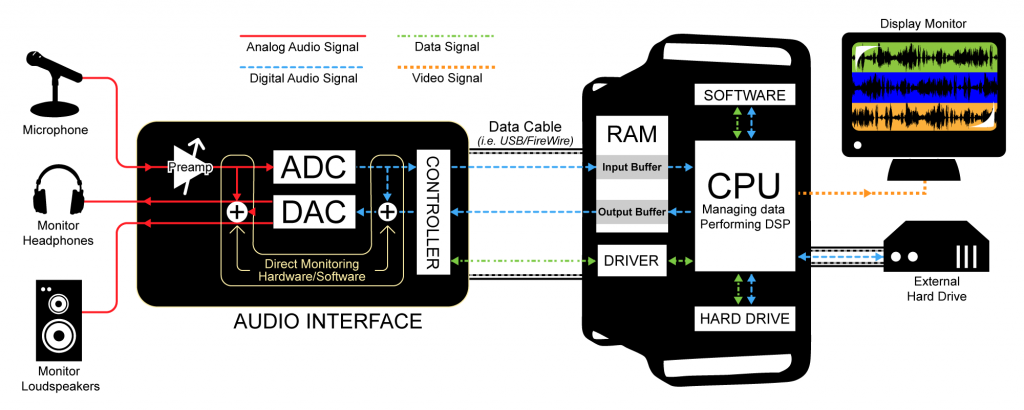
Figure 5.20 illustrates a recording session where a singer is singing into a microphone and monitoring the recording session with headphones. As the audio stream makes its way along the signal path, it passes through a variety of hardware and software, including the microphone, audio interface, audio driver, CPU, input and output buffers (which could be hardware or software), and hard drive. The CPU (central processing unit) is the main hardware workhorse of a computer, doing the actual computation that is required for tasks like accepting audio streams, running application programs, sending data to the hard drive, sending files to the printer, and so forth. The CPU works hand-in-hand with the operating system, which is the software program that manages which task is currently being worked on, like a conductor conducting an orchestra. Under the direction of the operating system, the CPU can give little slots of times to various processes, swapping among these processes very quickly so that it looks like each one is advancing normally. This way, multiple processes can appear to be running simultaneously.
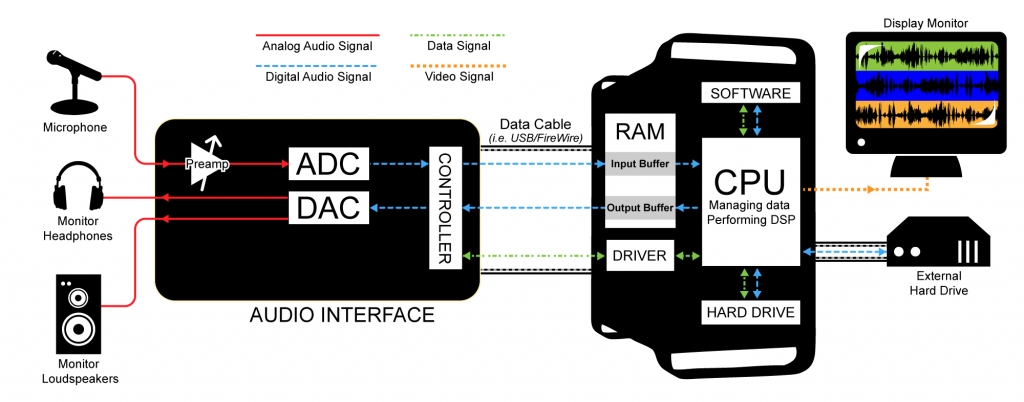
Now let’s get back to how a recording session works. During the recording session, the microphone, an analog device, receives the audio signal and sends it to the audio interface in analog form. The audio interface could be an external device or an internal sound card from GSEAV. The audio interface performs analog-to-digital conversion and passes the digital signal to the computer. The audio signal is received by the computer in a digital stream that is interpreted by a driver, a piece of software that allows two hardware devices to communicate. When an audio interface is connected to a computer, an appropriate driver must be installed in the computer so that the digital audio stream generated by the audio interface can be understood and located by the computer.
The driver interprets the audio stream and sends it to an audio input buffer in RAM. Saying that the audio buffer is in RAM implies that this is a software buffer. (The audio interface has a small hardware buffer as well, but we don’t need to go to this level of detail.) The audio input buffer provides a place where the audio data can be held until the CPU is ready to process it. Buffering of audio input is necessary because the CPU may not be able to process the audio stream as soon as it comes into the computer. The CPU has to handle other processes at the same time (monitor displays, operating system tasks, etc.). It also has to make a copy of the audio data on the hard disk because the digitizing and recording process generates too much data to fit in RAM. Moving back and forth to the hard drive is time consuming. The input buffer provides a holding place for the data until the CPU is ready for it.
Let’s follow the audio signal now to its output. In Figure 5.20, we’re assuming that you’re working on the audio in a program like Sonar or Logic. These audio processing programs serve as the user interface for the recording process. Here you can specify effects to be applied to tracks, start and stop the recording, and decide when and how to save the recording in permanent storage. The CPU performs any digital signal processing (DSP) called for by the audio processing software. For example, you might want reverb added to the singer’s voice. The CPU applies the reverb and then sends the processed data to the software output buffer. From here the audio data go back to the audio interface to be converted back to analog format and sent to the singer’s headphones or a set of connected loudspeakers. Possibly, the track of the singer’s voice could be mixed with a previously recorded instrumental track before it is sent to the audio interface and then to the headphones.
[wpfilebase tag=file id=119 tpl=supplement /]
For this recording process to run smoothly — without delays or breaks in the audio – you must choose and configure your drivers and hard drives appropriately. These practical issues are discussed further in Section 5.2.3.
Figure 5.20 gives an overview of the audio signal path in one scenario, but there are many details and variations that have not been discussed here. We’re assuming a software system such as Logic or Sonar is providing the mixer and DSP, but it’s possible for additional hardware to play these roles – a hardware mixing console, equalizer, or dynamics compressor, for example. Some professional grade software applications may even have additional external DSP processors to help offload some of the work from the CPU itself, such as with Pro Tools HD. This external gear could be analog or digital, so additional DAC/ADC conversions might be necessary. We also haven’t considered details like microphone pre-amps, loudspeakers and loudspeaker amps, data buses, and multiple channels. We refer the reader to the references at the end of the chapter for more information.
5.1.5 CPU and Hard Drive Considerations
As you work with digital audio, it’s important that you have some understanding of the demands on your computer’s CPU and hard drive. You might at times face problems saying drive corrupted or drive is not accessible, during such times make sure to contact a data recovery specialist with having yourself perform tasks trying to recover the data, as even a single step can lead to the file being completely erased from your system.
In general, the CPU is responsible for running all active processes on your computer. Processes take turns getting slices of time from the CPU so that they can all be making progress in their execution at the same time. You might have processes running on your computer at the same time you’re recording and not even be aware of it. For example, you may have automatic software updates activated. What if an automatic update tries to run while audio capture is in progress? The CPU is going to have to take some time to deal with that. If it’s dealing with a software update, it isn’t dealing with your audio stream.
Even if you make your best effort to turn off all other processes during recording, the CPU still has other important work to do that keeps it from returning immediately to the audio buffer. One of the CPU’s most important responsibilities during audio recording is writing audio data out to the hard drive. To understand how this works, it may be helpful to review briefly the different roles of RAM and hard disk memory with regard to a running program.
Ordinarily, we think of software programs operating according to the following scenario. Data is loaded into RAM, which is a space in memory temporarily allocated to a certain program. The program does computation on the data, changing it in some way. Since the RAM allocated to the program is released when the program finishes its computation, the data must be written out to the hard disk if you want a permanent copy. In this sense, RAM is considered volatile memory. For all intents and purposes, the data in RAM disappear when the program finishes execution.
But what if the program you’re running is an audio processing program like Logic or Sonar through which you’re recording audio? The recording process causes audio data to be read into RAM. Why can’t Sonar or Logic just store all the audio data in RAM until you’re done working on it and write it out to the hard disk when you’ve finished? The problem is that a very large amount of data is generated as the recording is being done – 176,400 bytes per second for CD quality audio. For a recording of any significant length, it isn’t feasible to store all the audio data in RAM. Thus, audio samples are constantly pulled from the RAM buffer by the CPU and placed on a hard drive. This takes a significant amount of the CPU’s time.
In order to keep up efficiently with the constant stream of data, the hard drive needs a dedicated space in which to write the audio data. Most audio recording programs automatically claim a large portion of hard drive space when you start recording. The size of this hard drive allocation is usually controllable in the preferences of your audio software. For example, if your software is configured to allocate 500 MB of hard drive space for each audio stream, 500 MB is immediately claimed on the hard drive when you start recording, and no other software may write to that space. If your recording uses 100 MB, the operating system returns the remaining 400 MB of space to be available to other programs. It’s important to make sure you configure the software to claim an appropriate amount of space. If your recording ends up needing more than 500 MB, the software begins dynamically finding new chunks of space on the hard drive to put the extra data. In this situation, it’s possible for dropouts to happen if sufficient space cannot be found fast enough. The problem is compounded by multitrack recording. Imagine what happens if you’re recording 24 tracks of audio at one time. The software has to find 24 blocks of space on the hard drive that are 500 MB in size. That’s 12 GB of free space that needs to be immediately and exclusively available.
One way to avoid problems is to dedicate a separate hard drive other than your startup drive for audio capture and data storage. That way you know that no other program will attempt to use the space on that drive. You also need to have a hard drive that is large enough and fast enough to handle this amount of sustained data being written, and often read back. In today’s technology, at least a 7200 RPM, one terabyte dedicated external hard drive with a high-speed connection should be sufficient.
5.1.6 Digital Audio File Types
[aside]In our discussion of file types, we’ll use capital letters like AIFF and WAV to refer to different formats. Generally there is a corresponding suffix, called a file extension, used on file names – e.g., .aiff or .wav. However, in some cases, more than one suffix can refer to the same basic file type. For example, .aiff and .aif, and .aifc are all variants of the AIFF format.[/aside]
You saw in the previous section that the digital audio stream moves through various pieces of software and hardware during a recording session, but eventually you’re going to want to save the stream as a file in permanent storage. At this point you have to decide the format in which to save the file. Your choice depends on how and where you’re going to use the recording.
Audio file formats differ along a number of axes. They can be free or proprietary, platform-restricted or cross-platform, compressed or uncompressed, container files or simple audio files, and copy-protected or unprotected. (Copy protection is more commonly referred to as digital rights management or DRM.)
Proprietary file formats are controlled by a company or an organization. The particulars of a proprietary format and how the format is produced are not made public and their use is subject to patents. Some proprietary files formats are associated with commercial software for audio processing. Such files can be opened and used only in the software with which they’re associated. Some examples are CWP files for Cakewalk Sonar, SES for Adobe Audition multitrack sessions, AUP projects for Audacity, and PTF for Pro Tools. These are project file formats that include meta-information about the overall organization of an audio project. Other proprietary formats – e.g., MP3 – may have patent restrictions on their use, but they have openly documented standards and can be licensed for use on a variety of platforms. As an alternative, there exist some free, open source audio file formats, including OGG and FLAC.
Platform-restricted files can be used only under certain operating systems. For example, WMA files run under Windows, AIFF files run under Apple OS, and AU files run under Unix and Linux. The MP3 format is cross-platform. AAC is a cross-platform format that has become widely popular from its use on phones, pad computers, digital radio, and video game consoles.
[aside]Pulse code modulation was introduced by British scientist A. Reeves in the 1930s. Reeves patented PCM as a way of transmitting messages in “amplitude-dichotomized, time-quantized” form – what we now call “digital.”[/aside]
You can’t tell from the file extension whether or not a file is compressed, and if it is compressed, you can’t necessarily tell what compression algorithm (called a codec) was used. There are both compressed and uncompressed versions of WAV, AIFF, and AU files. When you save an audio file, you can choose which type you want.The basic format for uncompressed audio data is called PCM (pulse code modulation). The term pulse code modulation is derived from the way in which raw audio data is generated and communicated. That is, it is generated by the process of sampling and quantization described in Section 5.1 and communicated as binary data by electronic pulses representing 0s and 1s. WAV, AIFF, AU, RAW, and PCM files can store uncompressed audio data. RAW files contain only the audio data, without even a header on the file.
One basic reason that WAV and AIFF files come in compressed and uncompressed versions is that, in reality, these are container file formats rather than simple audio files. A container file wraps a simple audio file in a meta-format which specifies blocks of information that should be included in the header along with the size and position of chunks of data following the header. The container file may allow options for the format of the actual audio data, including whether or not it is compressed. If the audio is compressed, the system that tries to open and play the container file must have the appropriate codec in order to decompress and play it. AIFF files are container files based on a standardized format called IFF. WAV files are based on the RIFF format. MP3 is a container format that is part of the more general MPEG standard for audio and video. WMA is a Windows container format. OGG is an open source, cross-platform alternative.
In addition to audio data, container files can include information like the names of songs, artists, song genres, album names, copyrights, and other annotations. The metadata may itself be in a standardized format. For example, MP3 files use the ID3 format for metadata.
Compression is inherent in some container file types and optional in others. MP3, AAC, and WMA files are always compressed. Compression is important if one of your main considerations is the ability to store lots of files. Consider the size of a CD quality audio file, which consists of two channels of 44,100 samples per second with two bytes per sample. This gives
$$!2\ast \frac{44000\: samples}{sec}\ast \frac{2\: bytes}{sample}\ast 60\frac{sec}{min}\ast 5\: min=52920000\: bytes\approx 50.5\: MB$$
[aside]Why are 52,920,000 bytes equal to about 50.5 MB? You might expect a megabyte to be 1,000,000 bytes, but in the realm of computers, things are generally done in powers of 2. Thus, we use the following definitions:
kilo = 210 = 1024
mega = 220 = 1,048,576
You should become familiar with the following abbreviations:
[table th=”0″ width=”100%”]
kilobits,kb,210 bits
kilobytes,kB,210 bytes
megabits,Mb,220 bits
megabytes,MB,220 bytes[/table]
Based on these definitions, 52,920,000 bytes is converted to megabytes by dividing by 1,048,576 bytes.
Unfortunately, usage is not entirely consistent. You’ll sometimes see “kilo” assumed to be 1000 and “mega” assumed to be 1,000,000, e.g., in the specification of the storage capacity of a CD.[/aside]
A five minute piece of music, uncompressed, takes up over 50 MB of memory. MP3 and AAC compression can reduce this to less than a tenth of the original size. Thus, MP3 files are popular for portable music players, since compression makes it possible to store many more songs.
Compression algorithms are of two basic types: lossless or lossy. In the case of a lossless compression algorithm, no audio information is lost from compression to decompression. The audio information is compressed, making the file smaller for storage and transmission. When it is played or processed, it is decompressed, and the exact data that was originally recorded is restored. In the case of a lossy compression algorithm, it’s impossible to get back exactly the original data upon decompression. Examples of lossy compression formats are MP3, AAC, Ogg Vorbis, and the m-law and A-law compression used in AU files. Examples of lossless compression algorithms include FLAC (Free Lossless Audio Codec), Apple Lossless, MPEG-4 ALS (Audio Lossless Coding), Monkey’s Audio, and TTA (True Audio). More details of audio codecs are given in Section 5.2.1.
With the introduction of portable music players, copy-protected audio files became more prevalent. Apple introduced iTunes in 2001, allowing users to purchase and download music from their online store. The audio files, encoded in a proprietary version of the AAC format and using the.m4p file extension, were protected with Apple’s FairPlay DRM system. DRM enforces limits on where the file can be played and whether it can be shared or copied. In 2009, Apple lifted restrictions on music sold from its iTunes store, offering an unprotected .m4a file as an alternative to .m4p. Copy-protection is generally embedded within container file formats like MP3. WMA (Windows Media Audio) files are another example, based on the Advanced Systems Format (ASF) and providing DRM support.
Common audio file types are summarized in Table 5.1.
[table caption=”Table 5.1 Common audio file types” width=”90%”]
File Type,Platform,File Extensions,Compression,Container,Proprietary,DRM
PCM,cross,.pcm,no,no,no,no
RAW,cross,.raw,no,no,no,no
WAV,cross,.wav,Optional (lossy),”yes, RIFF format”,no,no
AIFF,Mac,”.aif, .aiff,”,no,”yes, IFF format”,no,no
AIFF-C,Mac,.aifc,”yes, with various codecs (lossy)”,”yes, IFF format”,no,
CAF,Mac,.caf,yes,yes,no,no
AU,Unix/Linux,”.au, .snd”,optional m-law (lossy),yes,no,no
MP3,cross,.mp3,MPEG (lossy),yes,license required for~~distribution or sale of~~codec but not for use,optional
AAC,cross,”.m4a, .m4b, .m4p,~~.m4v, .m4r, .3gp,~~.mp4, .aac”,AAC (lossy),more of a compression~~standard than a container;~~ADIF is container ,license required for~~distribution or sale of~~codec but not for use,
WMA,Windows,.wma,WMA (lossy),yes,yes,optional
OGG Vorbis,cross,”.ogg, .oga”,Vorbis (lossy),yes,”no, open source”,optional
FLAC,cross,.flac,FLAC (lossless),yes,”no, open source”,optional
[/table]
AIFF and WAV have been the most commonly used file types in recent years. CAF files are an extension of AIFF files without AIFF’s 4 GB size limit. This additional file size was needed for all the looping and other metadata used in GarageBand and Logic.
[wpfilebase tag=file id=21 tpl=supplement /]
All along the way as you work with digital audio, you’ll have to make choices about the format in which you save your files. A general strategy is this:
- When you’re processing the audio in a software environment such as Audition, Logic, or Pro Tools, save your work in the software’s proprietary format until you’re finished working on it. These formats retain meta-information about non-destructive processes – filters, EQ, etc. – applied to the audio as it plays. Non-destructive processes do not change the original audio samples. Thus, they are easily undone, and you can always go back and edit the audio data in other ways for other purposes if needed.
- The originally recorded audio is the best information you have, so it’s always good to keep an uncompressed copy of this. Generally, you should keep as much data as possible as you edit an audio file, retaining the highest bit depth and sampling rate appropriate for the work.
- At the end of processing, save the file in the format suitable for your platform of distribution (e.g., CD, DVD, web, or live performance). This may be compressed or uncompressed, depending on your purposes.
5.2.1 Choosing an Appropriate Sampling Rate
Before you start working on a project you should decide what sampling rate you’re going to be working with. This can be a complicated decision. One thing to consider is the final delivery of your sound. If, for example, you plan to publish this content only as an audio CD, then you might choose to work with a 44,100 Hz sampling rate to begin with since that’s the required sampling rate for an audio CD. If you plan to publish your content to multiple formats, you might choose to work at a higher sampling rate and then convert down to the rate required by each different output format.
The sampling rate you use is directly related to the range of frequencies you can sample. With a sampling rate of 44,100 Hz, the highest frequency you can sample is 22,050 Hz. But if 20,000 Hz is the upper limit of human hearing, why would you ever need to sample a frequency higher than that? And why do we have digital systems able to work at sampling rates as high as 192,000 Hz?
First of all, the 20,000 Hz upper limit of human hearing is an average statistic. Some people can hear frequencies higher than 20 kHz, and others stop hearing frequencies after 16 kHz. The people who can actually hear 22 kHz might appreciate having that frequency included in the recording. It is, however, a fact that there isn’t a human being alive who can hear 96 kHz, so why would you need a 192 kHz sampling rate?
Perhaps we’re not always interested in the range of human hearing. A scientist who is studying bats, for example, may not be able to hear the high frequency sounds the bats make but may need to capture those sounds digitally to analyze them. We also know that musical instruments generate harmonic frequencies much higher than 20 kHz. Even though you can’t consciously hear those harmonics, their presence may have some impact on the harmonics you can hear. This might explain why someone with well-trained ears can hear the difference between a recording sampled at 44.1 kHz and the same recording sampled at 192 kHz.
The catch with recording at those higher sampling rates is that you need equipment capable of capturing frequencies that high. Most microphones don’t pick up much above 22 kHz, so running the signal from one of those microphones into a 96 kHz ADC isn’t going to give you any of the frequency benefits of that higher sampling rate. If you’re willing to spend more money, you can get a microphone that can handle frequencies as high at 140 kHz. Then you need to make sure that every further device handling the audio signal is capable of working with and delivering frequencies that high.
If you don’t need the benefits of sampling higher frequencies, the other reason you might choose a higher sampling rate is to reduce the latency of your digital audio system, as is discussed in Section 5.2.3.
A disadvantage to consider is that higher sampling rates mean more audio data, and therefore larger file sizes. Whatever your reasons for choosing a sampling rate, the important thing to remember is that you need to stick to that sampling rate for every audio file and every piece of equipment in your signal chain. Working with multiple sampling rates at the same time can cause a lot of problems.
5.2.2 Input Levels, Output Levels, and Dynamic Range
In this section, we consider how to set input and output levels properly and how these settings affect dynamic range.
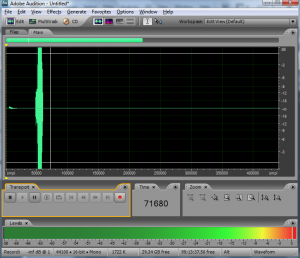
When you get ready to make a digital audio recording or set sound levels for a live performance, you typically test the input level and set it so that your loudest inputs don’t clip. Clipping occurs when the sound level is beyond the maximum input or output voltage level. It manifests itself as unwanted distortion or breaks in the sound. When capturing vocals, you can set the sound levels by asking a singer to sing the loudest note he thinks he’s going to sing in the whole piece, and make sure that the level meter doesn’t hit the limit. Figure 5.21 shows this situation in a software interface. The level meter at the bottom of the figure has hit the right hand side and thus has turned red, indicating that the input level is too high and clipping has occurred. In this case, you need to turn down the input level and test again before recording an actual take. The input level can be changed by a knob on your audio interface or, in the case of some advanced interfaces with digitally controlled analog preamplifiers, by a software interface accessible through your operating system. Figure 5.22 shows the input gain knob on an audio interface.

Let’s look more closely at what’s going on when you set the input level. Any hardware system has a maximum input voltage. When you set the input level for a recording session or live performance, you’re actually adjusting the analog input amplifier for the purpose of ensuring that the loudest sound you intend to capture does not generate a voltage higher than the maximum allowed by the system. However, when you set input levels, there’s no guarantee that the singer won’t sing louder than expected. Also, depending on the kind of sound you’re capturing, you might have transients – short loud bursts of sound like cymbal claps or drum beats – to account for. When setting the input level, you need to save some headroom for these occasional loud sounds. Headroom is loosely defined as the distance between your “usual” maximum amplitude and the amplitude of the loudest sound that can be captured without clipping. Allowing for sufficient headroom obviously involves some guesswork. There’s no guarantee that the singer won’t sing louder than expected, or some unexpectedly loud transients may occur as you record, but you make your best estimate for the input level and adjust later if necessary, though you might lose a good take to clipping if you’re not careful.
Let’s consider the impact that the initial input level setting has on the dynamic range of a recording. Recall from Section 5.1.2.4 that the quietest sound you can capture is relative to the loudest as a function of the bit depth. A 16-bit system provides a dynamic range of approximately 96 dB. This implies that, in the absence of environment noise, the quietest sounds that you can capture are about 96 dB below the loudest sounds you can capture. That 96 dB value is also assuming that you’re able to capture the loudest sound at the exact maximum input amplitude without clipping, but as we know leaving some headroom is a good idea. The quietest sounds that you can capture lie at what is called the noise floor. We could look at the noise floor from two directions, defining it as either the minimum amplitude level that can be captured or the maximum amplitude level of the noise in the system. With no environment or system noise, the noise floor is determined entirely by the bit depth, the only noise being quantization error.
[aside]
Why is the smallest value for a 16-bit sample -90.3 dB? Because $$20\log_{10}\left ( \frac{1}{32768} \right )=-90.3\: dB$$
[/aside]
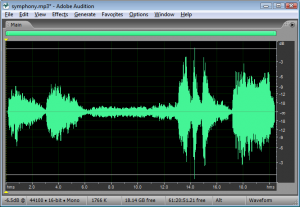
In the software interface shown in Figure 5.21, input levels are displayed in decibels-full-scale (dBFS). The audio file shown is a sine wave that starts at maximum amplitude, 0 dBFS, and fades all the way out. (The sine wave is at a high enough frequency that the display of the full timeline renders it as a solid shape, but if you zoom in you see the sine wave shape.) Recall that with dBFS, the maximum amplitude of sound for the given system is 0 dBFS, and increasingly negative numbers refer to increasingly quiet sounds. If you zoom in on this waveform and look at the last few samples (as shown in the bottom portion of Figure 5.23), you can see that the lowest sample values – the ones at the end of the fade – are -90.3 dBFS. This is the noise floor resulting from quantization error for a bit depth of 16 bits. A noise floor of -90.3 dBFS implies that any sound sample that is more than 90.3 dB below the maximum recordable amplitude is recorded as silence.
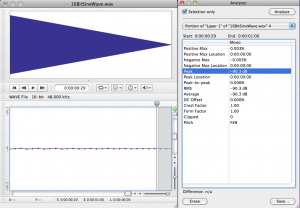
In reality, there is almost always some real-world noise in a sound capturing system. Every piece of audio hardware makes noise. For example, noise can arise from electrical interference on long audio cables or from less-than-perfect audio detection in microphones. Also, the environment in which you’re capturing the sound will have some level of background noise such as from the air conditioning system. The maximum amplitude of the noise in the environment or the sound-capturing system constitutes the real noise floor. Sounds below this level are masked by the noise. This means that either they’re muddied up with the noise, or you can’t distinguish them at all as part of the desired audio signal. In the presence of significant environmental or system noise during recording, the available dynamic range of a 16-bit recording is the difference between 0 dBFS and the noise floor caused by the environment and system noise. For example, if the noise floor is -70 dBFS, then the dynamic range is 70 dB. (Remember that when you subtract dBFS from dBFS, you get dB.)
So we’ve seen that the bit depth of a recorded audio file puts a fixed limit on the available dynamic range, and that this potential dynamic range can be made smaller by environmental noise. Another thing to be aware of is that you can waste some of the available dynamic range by setting your input levels in a way that leaves more headroom than you need. If you have 96 dB of dynamic range available but it turns out that you use only half of it, you’re squeezing your actual sound levels into a smaller dynamic range than necessary. This results in less accurate quantization than you could have had, and it puts more sounds below the noise floor than would have been there if you had used a greater part of your available dynamic range. Also, if you underuse your available dynamic range, you might run into problems when you try to run any long fades or other processes affecting amplitude, as demonstrated in the practical exercise “Bit Depth and Dynamic Range”linked in this section.
It should be clarified that increasing the input levels also increases any background environmental noise levels captured by a microphone, but can still benefit the signal by boosting it higher above any electronic or quantization noise that occurs downstream in the system. The only way to get better dynamic range over your air conditioner hum is to turn it off or get the microphone closer to the sound you want to record. This increases the level of the sound you want without increasing the level of the background noise.
[wpfilebase tag=file id=22 tpl=supplement /]
So let’s say you’re recording with a bit depth of 16 and you’ve set your input level just about perfectly to use all of that dynamic range possible in your recording. Will you actually be able to get the benefit of this dynamic range when the sound is listened to, considering the range of human hearing, the range of the sound you want to hear, and the background noise level in a likely listening environment? Let’s consider the dynamic range of human hearing first and the dynamic range of the types of things we might want to listen to. Though the human ear can technically handle a sound as loud as 120 dBSPL, such high amplitudes certainly aren’t comfortable to listen to, and if you’re exposed to sound at that level for more than a few minutes, you’ll damage your hearing. The sound in a live concert or dance club rarely exceeds 100 dBSPL, which is pretty loud to most ears. Generally, you can listen to a sound comfortably up to about 85 dBSPL. The quietest thing the human ear can ear is just above 0 dBSPL. The dynamic range between 85 dBSPL and 0 dBSPL is 85 dB. Thus, the 96 dB dynamic range provided by 16-bit recording effectively pushes the noise floor below the threshold of human hearing at a typical listening level.
We haven’t yet considered the noise floor of the listening environment, which is defined as the maximum amplitude of the unwanted background noise in the listening environment. The average home listening environment has a noise floor of around 50 dBSPL. With the dishwasher running and the air conditioner going, that noise floor could get up to 60 dBSPL. In a car (perhaps the most hostile listening environment) you could have a noise floor of 70 dBSPL or higher. Because of this high noise floor, car radio music doesn’t require more than about 25 dB of dynamic range. Does this imply that the recording bit depth should be dropped down to eight bits or even less for music intended to be listened to on the car radio? No, not at all.
Here’s the bottom line. You’ll almost always want to do your recordings in 16 bit sample sizes, and sometimes 24 bits or 32 bits are even better, even though there’s no listening environment on earth (other than maybe an anechoic chamber) that allows you the benefit of the dynamic range these bit depths provide. The reason for the large bit depths has to do with the processing you do on the audio before you put it into its final form. Unfortunately, you don’t always know how loud things will be when you capture them. If you guess low when setting your input level, you could easily get into a situation where most of the audio signal you care about is at the extreme quiet end of your available dynamic range, and fadeouts don’t work well because the signal too quickly fades below the noise floor. In most cases, a simple sound check and a bit of pre-amp tweaking can get you lined up to a place where 16 bits are more than enough. But if you don’t have the time, if you’ll be doing lots of layering and audio processing, or if you just can’t be bothered to figure things out ahead of time, you’ll probably want to use 24 bits. Just keep in mind that the higher the bit depth, the larger the audio files are on your computer.
An issue we’re not considering in this section is applying dynamic range compression as one of the final steps in audio processing. We mentioned that the dynamic range of car radio music’s listening environment is about 25 dB. If you play music that covers a wider dynamic range than 25 dB on a car radio, a lot of the soft parts are going to be drowned out by the noise caused by tire vibrations, air currents, etc. Turning up the volume on the radio isn’t a good solution, because it’s likely that you’ll have to make the loud parts uncomfortably loud in order to hear the quiet parts. In fact, the dynamic range of music prepared for radio play is often compressed after it has been recorded, as one of the last steps in processing. It might also be further compressed by the radio broadcaster. The dynamic range of sound produced for theatre can be handled in the same way, its dynamic range compressed as appropriate for the dynamic range of the theatre listening environment. Dynamic range compression is covered in Chapter 7.
5.2.3 Latency and Buffers
In Section 5.1.4, we looked at the digital audio signal path during recording. A close look at this signal path shows how delays can occur in between input and output of the audio signal, and how such delays can be minimized.
[wpfilebase tag=file id=120 tpl=supplement /]
Latency is the period of time between when an audio signal enters a system and when the sound is output and can be heard. Digital audio systems introduce latency problems not present in analog systems. It takes time for a piece of digital equipment to process audio data, time that isn’t required in fully analog systems where sound travels along wires as electric current at nearly the speed of light. An immediate source of latency in a digital audio system arises from analog-to-digital and digital-to-analog conversions. Each conversion adds latency on the order of milliseconds to your system. Another factor influencing latency is buffer size. The input buffer must fill up before the digitized audio data is sent along the audio stream to output. Buffer sizes vary by your driver and system, but a size of 1024 samples would not be usual, so let’s use that as an estimate. At a sampling rate of 44.1 kHz , it would take about 23 ms to fill a buffer with 1024 samples, as shown below.
$$!\frac{1\, sec}{44,100\, samples}\ast 1024\, samples\approx 23\: ms$$
Thus, total latency including the time for ADC, DAC, and buffer-filling is on the order of milliseconds. A few milliseconds of delay may not seem very much, but when multiple sounds are expected to be synchronized when they arrive at the listener, this amount of latency can be a problem, resulting in phase offsets and echoes.
Let’s consider a couple of scenarios in which latency can be a problem, and then look at how the problem can be dealt with. Imagine a situation where a singer is singing live on stage. Her voice is taken in by the microphone and undergoes digital processing before it comes out the loudspeakers. In this case, the sound is not being recorded, but there’s latency nonetheless. Any ADC/DAC conversions and audio processing along the signal path can result in an audible delay between when a singer sings into a microphone and when the sound from the microphone radiates out of a loudspeaker. In this situation, the processed sound arrives at the audience’s ears after the live sound of the singer’s voice, resulting in an audible echo. The simplest way to reduce the latency here is to avoid analog-to-digital and digital-to-analog conversions whenever possible. If you can connect two pieces of digital sound equipment using a digital signal transmission instead of an analog transmission, you can cut your latency down by at least two milliseconds because you’ll have eliminated two signal conversions.
Buffer size contributes to latency as well. Consider a scenario in which a singer’s voice is being digitally recorded (Figure 5.20). When an audio stream is captured in a digital device like a computer, it passes through an input buffer. This input buffer must be large enough to hold the audio samples that are coming in while the CPU is off somewhere else doing other work. When a singer is singing into a microphone, audio samples are being collected at a fixed rate – say 44,100 samples per second. The singer isn’t going to pause her singing and the sound card isn’t going to slow down the number of samples it takes per second just because the CPU is busy. If the input buffer is too small, samples have to be dropped or overwritten because the CPU isn’t there in time to process them. If the input buffer is sufficiently large, it can hold the samples that accumulate while the CPU is busy, but the amount of time it takes to fill up the buffer is added to the latency.
The singer herself will be affected by this latency is she’s listening to her voice through headphones as her voice is being digitally recorded (called live sound monitoring). If the system is set up to use software monitoring, the sound of the singer’s voice enters the microphone, undergoes ADC and then some processing, is converted back to analog, and reaches the singer’s ears through the headphones. Software monitoring requires one analog-to-digital and one digital-to-analog conversion. Depending on the buffer size and amount of processing done, the singer may not hear herself back in the headphones until 50 to 100 milliseconds after she sings. Even an untrained ear will perceive this latency as an audible echo, making it extremely difficult to sing on beat. If the singer is also listening to a backing track played directly from the computer, the computer will deliver that backing track to the headphones sooner than it can deliver the audio coming in live to the computer. (A backing track is a track that has already been recorded and is being played while the singer sings.)
[wpfilebase tag=file id=121 tpl=supplement /]
Latency in live sound monitoring can be avoided by hardware monitoring (also called direct monitoring). Hardware monitoring splits the newly digitized signal before sending it into the computer, mixing it directly into the output and eliminating the longer latencies caused by analog-to-digital conversion and input buffers (Figure 5.25). The disadvantage of hardware monitoring is that the singer cannot hear her voice with processing such as reverb applied. (Audio interfaces that offer direct hardware monitoring with zero-latency generally let you control the mix of what’s coming directly from the microphone and what’s coming from the computer. That’s the purpose of the monitor mix knob, circled in red in Figure 5.24.) When the mix knob is turned fully counterclockwise, only the direct input signals (e.g., from the microphone) are heard. When the mix knob is turned fully counterclockwise, only the signal from the DAW software is heard.

In general, the way to reduce latency caused by buffer size is to use the most efficient driver available for your system. In Windows systems, ASIO drivers are a good choice. ASIO drivers cut down on latency by allowing your audio application program to speak directly to the sound card, without having to go through the operating system. Once you have the best driver in place, you can check the interface to see if the driver gives you any control over the buffer size. If you’re allowed to adjust the size, you can find the optimum size mostly by trial and error. If the buffer is too large, the latency will be bothersome. If it’s too small, you’ll hear breaks in the audio because the CPU may not be able to return quickly enough to empty the buffer, and thus audio samples are dropped out.
With dedicated hardware systems (digital audio equipment as opposed to a DAW based on your desktop or laptop computer) you don’t usually have the ability to change the buffer size because those buffers have been fixed at the factory to match perfectly the performance of the specific components inside that device. In this situation, you can reduce the latency of the hardware by increasing your internal sampling rate. If this seems to hard for you to do you can get Laptop Repairs – Fix It Home Computer Repairs Brisbane. This may seem counterintuitive at first because a higher sampling rate means that you’re processing more data per second. This is true, but remember that the buffer sizes have been specifically set to match the performance capabilities of that hardware, so if the hardware gives you an option to run at a higher sampling rate, you can be confident that the system is capable of handling that speed without errors or dropouts. For a buffer of 1024 samples, a sampling rate of 192 kHz has a latency of about 5.3 ms, as shown below.
$$!1024\, samples\ast \frac{1}{192,000\, samples}\approx 5.3\, ms$$
If you can increase your sampling rate, you won’t necessarily get a better sound from your system, but the sound is delivered with less latency.
5.2.4 Word Clock
[wpfilebase tag=file id=122 tpl=supplement /]
When transmitting audio signals between digital audio hardware devices, you need to decide whether to transmit in digital or analog format. Transmitting in analog involves performing analog-to-digital conversions coming into the devices and digital-to-analog conversions coming out of the devices. As described in Section 5.2.1, you pay for this strategy with increased latency in your audio system. You may also pay for this in a loss of quality in your audio signal as a result of multiple quantization errors and a loss of frequency range if each digital device is using a different sampling rate. If you practice good gain structure (essentially, controlling amplitude changes from one device to the next) and keep all your sampling rates consistent, the loss of quality is minimal, but it is still something to consider when using analog interconnects. (See Chapter 8 for more on setting gain structure.)
Interconnecting these devices digitally can remove the latency and potential signal loss of analog interconnects, but digital transmission introduces a new set of problems, such as timing. There are several different digital audio transmission protocols, but all involve essentially the same basic process in handling data streams. The signal is transmitted as a stream of small blocks or frames of data containing the audio sample along with timing, channel information, and error correction bits. These data blocks are a constant stream of bits moving down a cable. The stream of bits is only meaningful when it gets split back up into the blocks containing the sample data in the same way it was sent out. If the stream is split up in the wrong place, the data block is invalid. To solve this problem, each digital device has a clock that runs at the speed of the sampling rate defined for the audio stream. This clock is called a word clock. Every time the clock ticks, the digital device grabs a new block of data – sometimes called an audio word – from the audio stream. If the device receiving the digital audio stream has a word clock that is running in sync with the word clock of the device sending the digital audio stream, each block that is transmitted is received and interpreted correctly. If the word clock of the receiving devices falls out of sync, it starts chopping up the blocks in the wrong place and the audio data will be invalid.
Even the most expensive word clock circuit is imperfect. This imperfection is measured in parts per million (ppm), and can be up to 50 ppm even in good quality equipment. At a sampling rate of 44.1 kHz, this equates to a potential drift of $$44100\ast \frac{50}{1000000}\approx 2.2$$ samples per second. Even if two word clocks start at precisely the same time, they are likely to drift at different rates and thus will eventually be out of sync. To avoid the errors that result from word clock drift, you need to synchronize the word clocks of all your digital devices. There are three basic strategies for word clock synchronization. The strategy you choose depends on the capability of the equipment you are using.
The first word clock synchronization strategy is to slave all your digital devices to a dedicated word clock generator. Any time you can go with a dedicated hardware solution, chances are good that the hardware is going to be pretty reliable. If the box only has to do one thing, it will probably be able to do it well. A dedicated word clock generator has a very stable word clock signal and several output connectors to send that word clock signal to all the devices in your system. It may also have the ability to generate and sync to other synchronization signals such as MIDI Time Code (MTC), Linear Time Code (LTC), and video black burst (the word clock equivalent for video equipment). An example of a dedicated synchronization tool is shown in Figure 5.26.

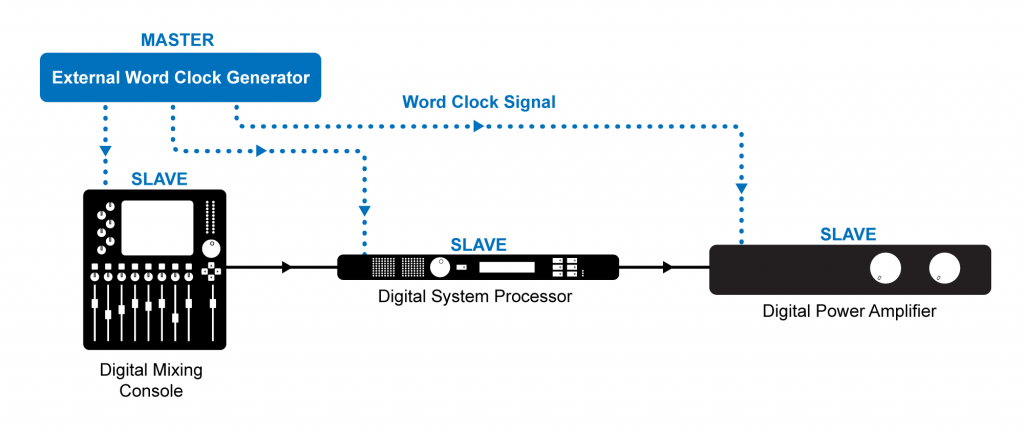
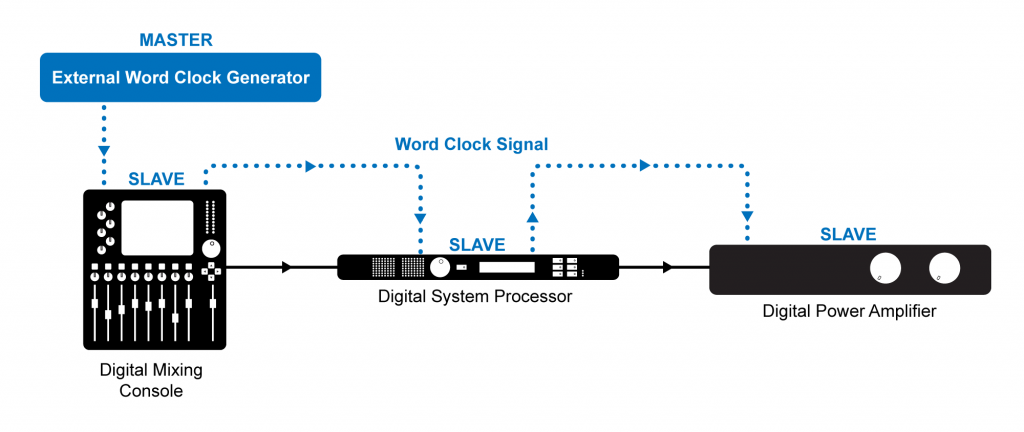
External word clock synchronization is typically accomplished using low impedance coaxial cable with BNC connectors. If your word clock generator has several outputs, you can connect each device directly to the clock master as shown in Figure 5.27. Otherwise you can connect the devices up in sequence from a single word clock output of your clock master shown in Figure 5.28.
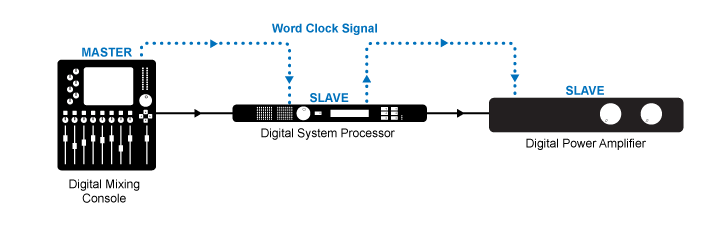
If you don’t have a dedicated word clock generator, you could choose one of the digital audio devices in your system to be the word clock master and slave all the other devices in your system to that clock using the external word clock connections as shown in Figure 5.29. The word clock of the device in your system is probably not as stable as a dedicated word clock generator (in that it may have a small amount of jitter), but as long as all the devices are following that clock, you will avoid any errors.
In some cases your equipment may not have external word clock inputs. This is common in less expensive equipment. In that situation you could go with a self-clocking solution where the first device in your signal chain is designated as the word clock master and each device in the signal chain is set to slave to the word clock signal embedded in the audio stream coming from the previous device in the signal chain, as shown in Figure 5.30.
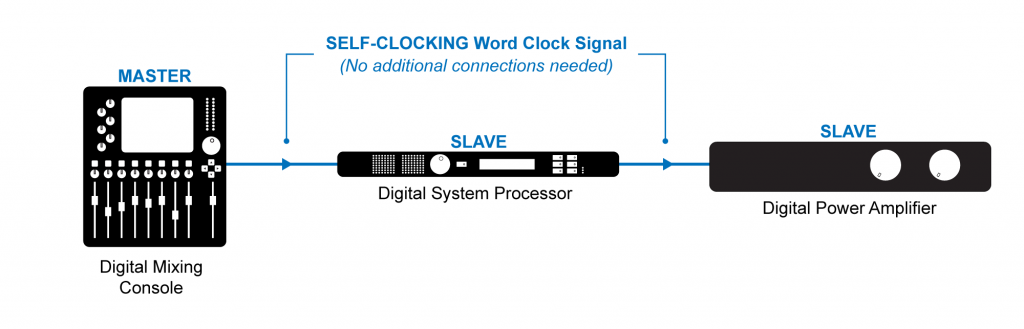
Regardless of the synchronization strategy you use, the goal is to have one word clock master with every other digital device in your system set to slave to the master word clock. If you set this up correctly, you should have no problems maintaining a completely digital signal path through your audio system and benefit from the decreased latency from input to output.