3.3.2 Equal Tempered vs. Just Tempered Intervals
In Section 3.1.4 we described the diatonic scales that are commonly used in Western music. These scales are built by making the frequency of each successive note $$\sqrt[12]{2}$$ times the frequency of the previous one. This is just one example of a temperament, a system for selecting the intervals between tones used in musical composition. In particular, it is called equal temperament or equal tempered intonation, and it produces equal tempered scales and intervals. While this is the intonation our ears have gotten accustomed to in Western music, it isn’t the only one, nor even the earliest. In this section we’ll look at an alternative method for constructing scales that dates back to Pythagoras in the sixth century B. C. – just tempered intonation – a tuning in which frequency intervals are chosen based upon their harmonic relationships.
First let’s look more closely and the equal tempered scales as a point of comparison. The diatonic scales described in Section 3.1.4 are called equal tempered because the factor by which the frequencies get larger remains equal across the scale. Table 3.13 shows the frequencies of the notes from C4 to C5, assuming that A4 is 440 Hz. Each successive frequency is $$\sqrt[12]{2}$$ times the frequency of the previous one.
[table caption=”Table 3.13 Frequencies of notes from C4 to C5″ width=”30%”]
Note,Frequency
C4,261.63 Hz
C4# (D4♭),277.18Hz
D4,293.66 Hz
D4# (E4♭),311.13 Hz
E4,329.63 Hz
F4,349.23 Hz
F4# (G4♭),369.99 Hz
G4,392.00 Hz
G4# (A4♭),415.30 Hz
A4,440.00 Hz
A4# (B4♭),466.16 Hz
B4,493.88 Hz
C5,523.25 Hz
[/table]
It’s interesting to note how the ratio of two frequencies in an interval affects our perception of the interval’s consonance or dissonance. Consider the ratios of the frequencies for each interval type, as shown in Table 3.14. Some of these ratios reduce very closely to fractions with small integers in the numerator and denominator. For example, the frequencies of G and C, a perfect fifth, reduce to approximately 3:2; and the frequencies of E and C, a major third, reduce to approximately 5:4. Pairs of frequencies that reduce to fractions such as these are the ones that sound more consonant, as indicated in the last column of the table.
[table caption=”Table 3.14 Ratio of beginning and ending frequencies in intervals” width=”80%”]
Interval,Notes in Interval,Ratio of Frequencies,,Common Perception of Interval
perfect unison,C,261.63/261.63 ,1,consonant
minor second,C C#,277.18/261.63 ,≈ 1.059/1,dissonant
major second,C D,293.66/261.63 ,≈ 1.122/1,dissonant
minor third,C D E♭,311.13/261.63 ,≈ 1.189/1 ≈ 6/5,consonant
major third,C D E,329.63/261.63 ,≈ 1.260/1 ≈ 5/4,consonant
perfect fourth,C D E F,349.23/261.63 ,≈ 1.335/1 ≈ 4/3,strongly consonant
augmented fourth,C D E F#,369.99/261.63 ,≈ 1.414/1,dissonant
perfect fifth,C D E F G,392.00/261.63 ,≈ 1.498/1 ≈ 3/2,strongly consonant
minor sixth,C D E F G A♭,415.30/261.63 ,≈ 1.587/1 ≈ 8/5,consonant
major sixth,C D E F G A,440.00/261.63 ,≈ 1.681/1 ≈ 5/3,consonant
minor seventh,C D E F G A B♭,466.16/261.63 ,≈ 1.781/1,dissonant
major seventh,C D E F G A B ,493.88/261.63 ,≈ 1.887/1,dissonant
perfect octave,C C,523.26/261.63 ,1,consonant
[/table]
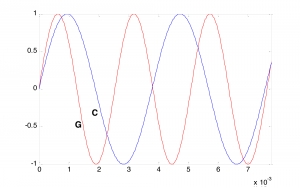
There’s a physical and mathematical explanation for this consonance. The fact that the frequencies of G and C have approximately a 3/2 ratio is visible in a graph of their sine waves. Figure 3.45 shows that three cycles of G fit almost exactly into two cycles of C. The sound waves fit together in an orderly pattern, and the human ear notices this agreement. But notice that we said the waves fit together almost exactly. The ratio of 392/261.63 is actually closer to 1.4983, not exactly 3/2, which is 1.5. Wouldn’t the intervals be even more harmonious if they were built upon the frequency relationships of natural harmonics?
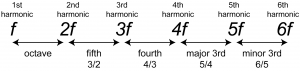
To consider how and why this might make sense, recall the definition of harmonic frequencies from Chapter 2. For a fundamental frequency $$f$$, the harmonic frequencies are $$1f$$, $$2f$$, $$3f$$, $$4f$$, and so forth. These are frequencies whose cycles do fit together exactly. As depicted in Figure 3.46, the ratio of the third to the second harmonic is $$\frac{3f}{2f}=\frac{3}{2}$$. This corresponds very closely, but not precisely, to what we have called a perfect fifth in equal tempered intonation – for example, the relationship between G and C in the key of C, or between D and G in the key of G. Similarly, the ratio of the fifth harmonic to the fourth is $$\frac{5f}{4f}=\frac{5}{4}$$, which corresponds to the interval we have referred to as a major third.
Just tempered intonations use frequencies that have these harmonic relationships. The Pythagoras diatonic scale is built entirely from fifths. The just tempered scale shown in Table 3.15 is a modern variant of Pythagoras’s scale. By comparing columns three and four, you can see how far the equal tempered tones are from the harmonic intervals. An interesting exercise would be to play a note in equal tempered frequency and then in just tempered frequency and see if you can notice the difference.
[table caption=”Table 3.15 Equal tempered vs. just tempered scales” width=”80%”]
Interval,Notes in Interval,Ratio of Frequencies in Equal Temperament,Ratio of Frequencies in Just Temperament
perfect unison,C,261.63/261.63 = 1.000,1/1 = 1.000
minor second,C C#,277.18/261.63 ≈ 1.059,16/15 ≈ 1.067
major second,C D,293.66/261.63 ≈ 1.122,9/8 = 1.125
minor third,C D E_,311.13/261.63 ≈ 1.189,6/5 = 1.200
major third,C D E,329.63/261.63 ≈ 1.260,5/4 ≈ 1.250
perfect fourth,C D E F,349.23/261.63 ≈ 1.335,4/3 ≈ 1.333
augmented fourth,C D E F#,369.99/261.63 ≈ 1.414,7/5 = 1.400
perfect fifth,C D E F G,392.00/261.63 ≈ 1.498,3/2 = 1.500
minor sixth,C D E F G A♭,415.30/261.63 ≈ 1.587,8/5 = 1.600
major sixth,C D E F G A,440.00/261.63 ≈ 1.682,5/3 ≈ 1.667
minor seventh,C D E F G A B♭,466.16/261.63 ≈ 1.782,7/4 = 1.750
major seventh,C D E F G A B ,493.88/261.63 ≈ 1.888,15/8 = 1.875
perfect octave,C C,523.26/261.63 = 2.000,2/1 = 2.000
[/table]
3.3.3 Experimenting with Music in Max
Max (and its open source counterpart, PD) is a powerful environment for experimenting with sound and music. We use one of our own learning supplements, a Max patcher for generating scales (3.1.4), as an example of the kinds of programs you can write.
When you open this patcher, it is in presentation mode (Figure 3.47), as indicated by the drop-down menu in the bottom right corner. In presentation mode, the patcher is laid out in a user-friendly format, showing only the parts of the interface that you need in order to run the tutorial, which in this case allows you to generate major and minor scales in any key you choose. You can change to programming mode (Figure 3.48) by choosing this option from the drop-down menu.
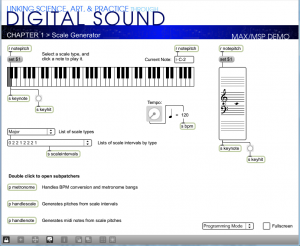
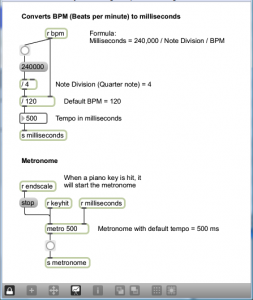
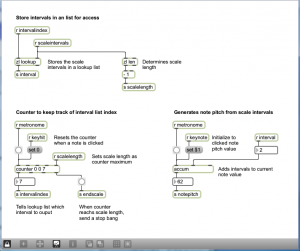
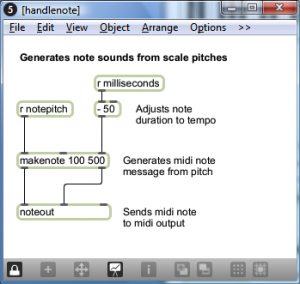
Programming mode reveals more of the Max objects used in the program. You can now see that the scale-type menu is connected to a list object. This list changes in accordance with the selection, each time giving the number of semitones between consecutive notes on the chosen type of scale. You can also see that the program is implemented with a number of send, receive, and patcher objects. Send and receive objects pass data between them, as the names imply. Objects named s followed by an argument, as in s notepitch, are the send objects. Objects named r followed by an argument, as in r notepitch, are the receive objects. Patcher objects are “subpatchers” within the main program, their details hidden so that the main patcher is more readable. You can open a patcher object in programming mode by double-clicking on it. The metronome, handlescale, and handlenote patcher objects are open in Figure 3.49, Figure 3.50, and Figure 3.51.
In this example, you still can’t see the details of how messages are being received and processed. To do so, you have to unlock the main patcher window by clicking the lock icon in the bottom left corner. This puts you in a mode where you can inspect and even edit objects. The main patcher is unlocked in Figure 3.52. You must have the full Max application, not just the runtime, to go into full programming mode.
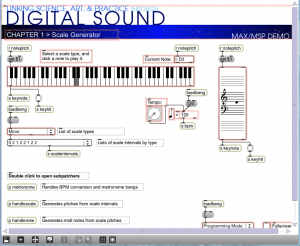
With all the patcher objects exposed and the main patcher unlocked, you can now see how the program is initialized and how the user is able to trigger the sending and receiving of messages by selecting from a menu, turning the dial to set a tempo, and clicking the mouse on the keyboard display. Here’s how the program runs:
- The loadbang object is triggered when the program begins. It is used to initialize the tempo to 120 bpm and to set the default MIDI output device. Both of these can be changed by the user.
- The user can select a type of scale from a menu. The list of intervals is set accordingly and sent in the variable scalesintervals, to be received by the handlescale patcher object.
- The user can select a tempo through the dial object. The input value is sent to the metronome patcher object to determine the timing of the notes played in the scale.
- The user can click a key on the keyboard object. This initiates the playing of a scale by sending a keyhit message to both the metronome and the handlescale patcher.
- When the metronome patcher receives the keyhit message, it begins sending a tick every n milliseconds. The value of n is calculated based on the bpm value. Each tick of the metronome is what Max calls a bang message, which is used to trigger buttons and set actions in motion. In this case, the bang sets off a counter in the handlescale patcher, which counts out the correct number of notes as it plays a scale. The number of notes to play for a given type of scale is determined by a lookup list in the zl object, a multipurpose list processing object.
- The pitch of the note is determined by setting the keynote to the correct one and then accumulating offsets from there. As the correct notepitch is set for each successive note, it is sent to the handlenote patcher, which makes a MIDI message from this information and outputs the MIDI note. To understand this part of the patcher completely, you need to know a little bit about MIDI messages, which we don’t cover in detail until Chapter 6. It suffices for now to understand that middle C is sent as a number message with the value 60. Thus, a C major scale starting on middle C is created from the MIDI notes 60, 62, 64, 65, 67, 69, 71, and 72.
[wpfilebase tag=file id=36 tpl=supplement /]
Max has many types of built-in objects with specialized functions. We’ve given you a quick overview of some of them in this example. However, as a beginning Max programmer, you can’t always tell from looking at an object in programming mode just what type of object it is and how it functions. To determine the types of objects and look more closely at the implementation, you need to unlock the patcher, as shown in Figure 3.52. Then if you select an object and right click on it, you get a menu that tells the type of object at the top. In the example in Figure 3.53, the object is a kslider. From the context menu, you can choose to see the Help or an Inspector associated with the object. To see the full array of Max built-in objects, go to Max Help from the main Help menu, and from there to Object by Function.

3.3.4 Experimenting with Music in MATLAB
Chapter 2 introduces some command line arguments for evaluating sine waves, playing sounds, and plotting graphs in MATLAB. For this chapter, you may find it more convenient to write functions in an external program. Files that contain code in the MATLAB language are called M-files, ending in the .m suffix. Here’s how you proceed when working with M-files:
- Create an M-file using MATLAB’s built-in text editor (or any text editor)
- Write a function in the M-file.
- Name the M-file fun1.m where fun1 is the name of function in the file.
- Place the M-file in your current MATLAB directory.
- Call the function from the command line, giving input arguments as appropriate and accepting the output by assigning it to a variable if necessary.
[wpfilebase tag=file id=53 tpl=supplement /]
The M-file can contain internal functions that are called from the main function. We refer you to MATLAB’s Help for details of syntax and program structure, but offer the program in Algorithm 3.1 to get you started. This program allows the user to create major and minor scales beginning with a start note. The start note is represented as a number of semitones offset from middle C. The function plays eight seconds of sound at a sampling rate of 44,100 samples per second and returns the raw data to the user, where it can be assigned to a variable on the command line if desired.
function outarray = MakeScale(startnoteoffset, isminor) %outarray is an array of sound samples on the scale of (-1,1) %outarray contains the 8 notes of a diatonic musical scale %each note is played for one second %the sampling rate is 44100 samples/s %startnoteoffset is the number of semitones up or down from middle C at %which the scale should start. %If isminor == 0, a major scale is played; otherwise a minor scale is played. sr = 44100; s = 8; outarray = zeros(1,sr*s); majors=[0 2 4 5 7 9 11 12]; minors=[0 2 3 5 7 8 10 12]; if(isminor == 0) scale = majors; else scale = minors; end scale = scale/12; scale = 2.^scale; %.^ is element-by-element exponentiation t = [1:sr]/sr; %the statement above is equivalent to startnote = 220*(2^((startnoteoffset+3)/12)) scale = startnote * scale; %Yes, ^ is exponentiation in MATLAB, rather than bitwise XOR as in C++ for i = 1:8 outarray(1+(i-1)*sr:sr*i) = sin((2*pi*scale(i))*t); end sound(outarray,sr);
Algorithm 3.1 Generating scales
The variables majors and minors hold arrays of integers, which can be created in MATLAB by placing the integers between square brackets, with no commas separating them. This is useful for defining, for each note in a diatonic scale, the number of semitones that the note is away from the key note.
[wpfilebase tag=file id=55 tpl=supplement /]
The lineThe variable scale is also an array, the same length as majors and minors (eight elements, because eight notes are played for the diatonic scale). Say that a major scale is to be created. Each element in scale is set to $$2^{\frac{majors\left [ i \right ]}{12}}$$, where majors[i] is the original value of element i in the array majors. (Note that arrays are numbered beginning at 1 in MATLAB.) This sets scale equal to $$\left [ 1,2^{\frac{2}{12}},2^{\frac{4}{12}},2^{\frac{5}{12}},2^{\frac{7}{12}},2^{\frac{9}{12}},2^{\frac{11}{12}} \right ]$$. When the start note is multiplied by each of these numbers, one at a time, the frequencies of the notes in a scale are produced.
x = [1:sr]/sr;
creates an array of 44,100 points between 0 and 1 at which the sine function is evaluated. (This is essentially equivalent to x = linspace(0,1, sr), which we used in previous examples.)
A3 with a frequency of 220 Hz is used as a reference point from which all other frequencies are built. Thus
startnote = 220*(2^((startnoteoffset+3)/12));
sets the start note to be middle C plus the user-defined offset.
In the for loop that repeats for eight seconds, the statement
outarray(1+(i-1)*sr:sr*i) = sin((2*pi*scale(i))*t);
writes the sound data into the appropriate section of outarray. It generates these samples by evaluating a sine function of the appropriate frequency across the 44,100-element array x. This statement is an example of how conveniently MATLAB handles array operations. A single call to a sine function can be used to evaluate the function over an entire array of values. The statement
scale = scale/12;
works similarly, dividing each element in the array scale by 12. The statement
scale = 2.^scale;
is also an element-by-element array operation, but in this case a dot has to be added to the exponentiation operator since ^ alone is matrix exponentiation, which can have only an integer exponent.
3.3.5 Experimenting with Music in C++
Algorithm 3.2 is a C++ program analogous to the MATLAB program for generating scales. It uses the same functions for writing to the sound device as used the last section of Chapter 2. You can try your hand at a similar program by doing one of the suggested programming exercises. The first exercise has you generate (or recognize) chords of seven types in different keys. The second exercise has you generate equal tempered and just tempered scales and listen to the result to see if your ears can detect the small differences in frequencies. Both of these programs can be done in either MATLAB or C++.
[wpfilebase tag=file id=83 tpl=supplement /]
[wpfilebase tag=file id=79 tpl=supplement /]
[wpfilebase tag=file id=81 tpl=supplement /]
//This program works under the OSS library
#include <sys/ioctl.h> //for ioctl()
#include <math.h> //sin(), floor()
#include <stdio.h> //perror
#include <fcntl.h> //open, O_WRONLY
#include <linux/soundcard.h> //SOUND_PCM*
#include <iostream>
#include <stdlib.h>
using namespace std;
#define LENGTH 1 //number of seconds
#define RATE 44100 //sampling rate
#define SIZE sizeof(short) //size of sample, in bytes
#define CHANNELS 1 // number of stereo channels
#define PI 3.14159
#define SAMPLE_MAX 32767 // should this end in 8?
#define MIDDLE_C 262
#define SEMITONE 1.05946
enum types {BACK = 0, MAJOR, MINOR};
double getFreq(int index){
return MIDDLE_C * pow(SEMITONE, index-1);
}
int getInput(){
char c;
string str;
int i;
while ((c = getchar()) != '\n' && c != EOF)
str += c;
for (i = 0; i < str.length(); ++i)
str.at(i) = tolower(str.at(i));
if (c == EOF || str == "quit")
exit(0);
return atoi(str.c_str());
}
int getIndex()
{
int input;
cout
<< "Choose one of the following:\n"
<< "\t1) C\n"
<< "\t2) C sharp/D flat\n"
<< "\t3) D\n"
<< "\t4) D sharp/E flat\n"
<< "\t5) E\n"
<< "\t6) F\n"
<< "\t7) F sharp/G flat\n"
<< "\t8) G\n"
<< "\t9) G sharp/A flat\n"
<< "\t10) A\n"
<< "\t11) A sharp/B flat\n"
<< "\t12) B\n"
<< "\tor type quit to quit\n";
input = getInput();
if (! (input >= BACK && input <= 12))
return -1;
return input;
}
void writeToSoundDevice(short buf[], int buffSize, int deviceID) {
int status;
status = write(deviceID, buf, buffSize);
if (status != buffSize)
perror("Wrote wrong number of bytes\n");
status = ioctl(deviceID, SOUND_PCM_SYNC, 0);
if (status == -1)
perror("SOUND_PCM_SYNC failed\n");
}
int getScaleType(){
int input;
cout
<< "Choose one of the following:\n"
<< "\t" << MAJOR << ") for major\n"
<< "\t" << MINOR << ") for minor\n"
<< "\t" << BACK << ") to back up\n"
<< "\tor type quit to quit\n";
input = getInput();
return input;
}
void playScale(int deviceID){
int arraySize, note, steps, index, scaleType;
int break1; // only one half step to here
int break2; // only one half step to here
int t, off;
double f;
short *buf;
arraySize = 8 * LENGTH * RATE * CHANNELS;
buf = new short[arraySize];
while ((index = getIndex()) < 0)
cout << "Input out of bounds. Please try again.\n";
f = getFreq(index);
while ((scaleType = getScaleType()) < 0)
cout << "Input out of bounds. Please try again.\n";
switch (scaleType) {
case MAJOR :
break1 = 3;
break2 = 7;
break;
case MINOR :
break1 = 2;
break2 = 5;
break;
case BACK :
return;
default :
playScale(deviceID);
}
arraySize = LENGTH * RATE * CHANNELS;
for (note = off = 0; note < 8; ++note, off += t) {
if (note == 0)
steps = 0;
else if (note == break1 || note == break2)
steps = 1;
else steps = 2;
f *= pow(SEMITONE, steps);
for (t = 0; t < arraySize; ++t)
buf[t + off] = floor(SAMPLE_MAX*sin(2*PI*f*t/RATE));
}
arraySize = 8 * LENGTH * RATE * SIZE * CHANNELS;
writeToSoundDevice(buf, arraySize, deviceID);
delete buf;
return;
}
int main(){
int deviceID, arg, status, index;
deviceID = open("/dev/dsp", O_WRONLY, 0);
if (deviceID < 0)
perror("Opening /dev/dsp failed\n");
arg = SIZE * 8;
status = ioctl(deviceID, SOUND_PCM_WRITE_BITS, &arg);
if (status == -1)
perror("Unable to set sample size\n");
arg = CHANNELS;
status = ioctl(deviceID, SOUND_PCM_WRITE_CHANNELS, &arg);
if (status == -1)
perror("Unable to set number of channels\n");
arg = RATE;
status = ioctl(deviceID, SOUND_PCM_WRITE_RATE, &arg);
if (status == -1)
perror("Unable to set sampling rate\n");
while (true)
playScale(deviceID);
}
Algorithm 3.2
3.3.6 Experimenting with Music in Java
[wpfilebase tag=file id=128 tpl=supplement /]
Let’s try making chords in Java as we did in C++. We’ll give you the code for this first exercise to get you started, and then you can try some exercises on your own. The “Chords in Java” program plays a chord selected from the list shown in Figure 3.54. The program contains two Java class files, one called Chord and the other called ChordApp. The top level class (i.e., the one that includes the main function) is the ChordApp class. The ChordApp class is a subclass of the JPanel, which is a generic window container. The JPanel provides functionality to display a window as a user interface. The constructor of the ChordApp class creates a list of radio buttons and displays the window with these options (Figure 3.54). When the user selects a type of chord, the method playChord() is called through the Chord class (line 138).
The ChordApp class contains the method playChord (line 7), which is a variation of the code shown in the MATLAB section. In the playChord method, the ChordApp object creates a Chord object, initializing it with the array scale, which contains the list of notes to be played in the chord. These notes are summed in the Chord class in lines 46 to 48.
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class ChordApp extends JPanel implements ActionListener {
public static void playChord(String command)
{/**Method that decides which Chord to play */
float[] major7th = {0, 4, 7, 11};
float[] minor7th = {0, 3, 7, 10};
float[] domin7th = {0, 4, 7, 10};
float[] dimin7th = {0, 3, 6, 10};
float[] majorTri = {0, 4, 7};
float[] minorTri = {0, 3, 7};
float[] augmeTri = {0, 4, 8};
float[] diminTri = {0, 3, 6};
float[] scale;
if (command == "major7th")
scale = major7th;
else if (command == "minor7th")
scale = minor7th;
else if (command == "domin7th")
scale = domin7th;
else if (command == "dimin7th")
scale = dimin7th;
else if (command == "majorTri")
scale = majorTri;
else if (command == "minorTri")
scale = minorTri;
else if (command == "augmeTri")
scale = augmeTri;
else
scale = diminTri;
float startnote = 220*(2^((2+3)/12));
for(int i=0;i<scale.length;i++){
scale[i] = scale[i]/12;
scale[i] = (float)Math.pow(2,scale[i]);
scale[i] = startnote * scale[i];
}
//once we know which Chord to play, we call the Chord function
Chord chord = new Chord(scale);
chord.play();
}
public ChordApp() {
super(new BorderLayout());
try {
UIManager.setLookAndFeel(UIManager.getSystemLookAndFeelClassName());
SwingUtilities.updateComponentTreeUI(this);
} catch (Exception e) {
System.err.println(e);
}
JRadioButton maj7thButton = new JRadioButton("Major Seventh");
maj7thButton.setActionCommand("major7th");
JRadioButton min7thButton = new JRadioButton("Minor Seventh");
min7thButton.setActionCommand("minor7th");
JRadioButton dom7thButton = new JRadioButton("Dominant Seventh");
dom7thButton.setActionCommand("domin7th");
JRadioButton dim7thButton = new JRadioButton("Diminished Seventh");
dim7thButton.setActionCommand("dimin7th");
JRadioButton majTriButton = new JRadioButton("Major Triad");
majTriButton.setActionCommand("majorTri");
JRadioButton minTriButton = new JRadioButton("Minor Triad");
minTriButton.setActionCommand("minorTri");
JRadioButton augTriButton = new JRadioButton("Augmented Triad");
augTriButton.setActionCommand("augmeTri");
JRadioButton dimTriButton = new JRadioButton("Diminished Triad");
dimTriButton.setActionCommand("diminTri");
ButtonGroup group = new ButtonGroup();
group.add(maj7thButton);
group.add(min7thButton);
group.add(dom7thButton);
group.add(dim7thButton);
group.add(majTriButton);
group.add(minTriButton);
group.add(augTriButton);
group.add(dimTriButton);
maj7thButton.addActionListener(this);
min7thButton.addActionListener(this);
dom7thButton.addActionListener(this);
dim7thButton.addActionListener(this);
majTriButton.addActionListener(this);
minTriButton.addActionListener(this);
augTriButton.addActionListener(this);
dimTriButton.addActionListener(this);
JPanel radioPanel = new JPanel(new GridLayout(0, 1));
radioPanel.add(maj7thButton);
radioPanel.add(min7thButton);
radioPanel.add(dom7thButton);
radioPanel.add(dim7thButton);
radioPanel.add(majTriButton);
radioPanel.add(minTriButton);
radioPanel.add(augTriButton);
radioPanel.add(dimTriButton);
add(radioPanel, BorderLayout.LINE_START);
setBorder(BorderFactory.createEmptyBorder(20,20,20,20));
}
public static void main(String[] args) {
javax.swing.SwingUtilities.invokeLater(new Runnable() {
public void run() {
ShowWindow();
}
});
}
private static void ShowWindow() {
JFrame frame = new JFrame("Chords App");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
JComponent newContentPane = new ChordApp();
newContentPane.setOpaque(true); //content panes must be opaque
frame.setContentPane(newContentPane);
frame.pack();
frame.setVisible(true);
}
/** Listens to the radio buttons. */
public void actionPerformed(ActionEvent e) {
ChordApp.playChord(e.getActionCommand());
}
}
Algorithm 3.3 ChordApp class
import javax.sound.sampled.AudioFormat;
import javax.sound.sampled.AudioSystem;
import javax.sound.sampled.SourceDataLine;
import javax.sound.sampled.LineUnavailableException;
public class Chord {
float[] Scale;
public Chord(float[] scale) {
Scale=scale;
}
public void play() {
try {
makeChord(Scale);
} catch (LineUnavailableException lue) {
System.out.println(lue);
}
}
private void makeChord(float[] scale)
throws LineUnavailableException
{
int freq = 44100;
float[] x=new float[(int)(freq)];
byte[] buf;
AudioFormat audioF;
for(int i=0;i<x.length;i++){
x[i]=(float)(i+1)/freq;
}
buf = new byte[1];
audioF = new AudioFormat(freq,8,1,true,false);
SourceDataLine sourceDL = AudioSystem.getSourceDataLine(audioF);
sourceDL = AudioSystem.getSourceDataLine(audioF);
sourceDL.open(audioF);
sourceDL.start();
for (int j=0;j<x.length;j++){
buf[0]= 0;
for(int i=0;i<scale.length;i++){
buf[0]=(byte)(buf[0]+(Math.sin((2*Math.PI*scale[i])*x[j])*10.0))
}
sourceDL.write(buf,0,1);
}
sourceDL.drain();
sourceDL.stop();
sourceDL.close();
}
}
Algorithm 3.4 Chord class
[wpfilebase tag=file id=87 tpl=supplement /]
[wpfilebase tag=file id=85 tpl=supplement /]
As another exercise, you can try to play and compare equal vs. just tempered scales, the same program exercise linked in the C++ section above.
The last exercise associated with this section, you’re asked to create a metronome-type object that creates a beat sound according to the user’s specifications for tempo. You may want to borrow something similar to the code in the ChordApp class to create the graphical user interface.
[separator top=”1″ bottom=”0″ style=”none”]