You have seen in previous chapters how sounds are generally composed of multiple frequency components. Sometimes it’s desirable to increase the level of some frequencies or decrease others. To deal with frequencies, or bands of frequencies, selectively, we have to separate them out. This is done by means of filters. The frequency processing tools in the following sections are all implemented with one type of filter or another.
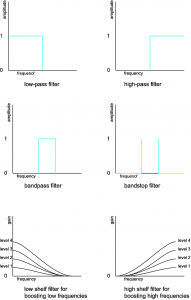
There are a number of ways to categorize filters. If we classify them according to what frequencies they attenuate, then we have these types of band filters:
- low-pass filter – retains only frequencies below a given threshold
- high-pass filter – retains only frequencies above a given threshold
- bandpass filter – retains only frequencies within a given frequency band
- bandstop filter – eliminates frequencies within a given frequency band
- comb filter – attenuates frequencies in a manner that, when graphed in the frequency domain, has a “comb” shape. That is, multiples of some fundamental frequency are attenuated across the audible spectrum
- peaking filter – boosts or attenuates frequencies in a band
- shelving filters
- low-shelf filter – boosts or attenuates low frequencies
- high-shelf filter – boosts or attenuates high frequencies
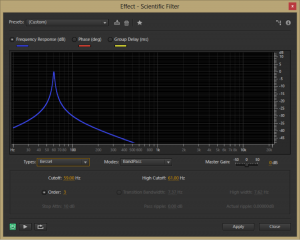
Filters that have a known mathematical basis for their frequency response graphs and whose behavior is therefore predictable at a finer level of detail are sometimes called scientific filters. This is the term Adobe Audition uses for Bessel, Butterworth, Chebyshev, and elliptical filters. The Bessel filter’s frequency response graph is shown in Figure 7.2
If we classify filters according to the way in which they are designed and implemented, then we have these types:
- IIR filters – infinite impulse response filters
- FIR filters – finite impulse response filters
Adobe Audition uses FIR filters for its graphic equalizer but IIR filters for its parametric equalizers (described below.) This is because FIR filters give more consistent phase response, while IIR filters give better control over the cutoff points between attenuated and non-attenuated frequencies. The mathematical and algorithmic differences of FIR and IIR filters are discussed in Section 3. The difference between designing and implementing filters in the time domain vs. the frequency domain is also explained in Section 3.
Convolution filters are a type of FIR filter that can apply reverberation effects so as to mimic an acoustical space. The way this is done is to record a short loud burst of sound in the chosen acoustical space and use the resulting sound samples as a filter on the sound to which you want to apply reverb. This is described in more detail in Section 7.1.6.