The inverse square law says, in essence, that for two points at distance $$r_{0}$$ and $$r_{1}$$ from a point sound source, where $$r_{1}>r_{0}$$, the sound intensity diminishes by $$20\log_{10}\left ( \frac{r_{0}}{r_{1}}\right )$$ dB. To derive the inverse square law mathematically, we can use the formula for the surface area of a sphere, $$4\pi r^{2}$$, where r is the radius of the sphere. Notice that in Figure 4.18, the radius of the sphere is also the distance from the sound source to the surface of that sphere. Recall that intensity is defined as power per unit area – that is, power proportional to the area over which it is spread. As the sound gets farther from the source, it spreads out over a larger area. At any distance r from the source, $$I=\frac{P}{4\pi r^{2}}$$ where I is intensity and P is the power at the source. Notice that if you increase the radius of the sphere by a factor of n, gets smaller by a factor of $$n^{2}$$. Thus, I is proportional to the inverse of $$r^{2}$$, which can be stated mathematically as $$I \propto \frac{1}{r^{2}}$$. We can state this more completely as
[equation caption=”Equation 4.16 Ratio of sound intensity comparing one location to another”]
$$!I_{1}=I_{0}\ast \left ( \frac{r_{0}}{r_{1}} \right )^{2}$$
where $$I_{0}$$ is the intensity of the sound at the first location,
$$I_{1}$$ is the intensity of the sound at the second location,
$$r_{0}$$ is the initial distance from the sound,
and $$r_{1}$$ is the new distance from the sound.
[/equation]
We usually represent intensities in decibels, so let’s convert to decibels applying the definition of dBSIL.
$$!10\log_{10}I_{1}=10\log_{10}\left ( I_{0}\ast \left ( \frac{r_{0}}{r_{1}} \right )^{2} \right )$$
$$!10\log_{10}I_{1}=10\log_{10}I_{0}+10\log_{10}\left ( \frac{r_{0}}{r_{1}} \right )^{2}$$
Thus
[equation caption=”Equation 4.17″]
$$!I_{1\, dBSIL}-I_{0\,dBSIL}=20\log_{10}\left ( \frac{r_{0}}{r_{1}} \right )dB$$
where $$I_{0\,dBSIL}$$ is the intensity of the sound at the first location in decibels,
$$!I_{1\, dBSIL}$$ is the intensity of the sound at the second location in decibels,
$$r_{0}$$ is the initial distance from the sound,
$$r_{1}$$ and is the new distance from the sound
[/equation]
Recall that when you subtract dBSIL from dBSIL, you get dB.
Based on the inverse square law, it is easy to prove that if you double the distance from the sound, you get about a 6 dB decrease (as listed in Table 4.5).
In Section 4.2.2.1, we looked at how the PAG is determined so that a sound engineer can know the limits of the gain he can apply to the sound without getting feedback. You can understand why feedback happens and how it can be prevented by applying the inverse square law.
First, we can derive an equation for the sound level that comes from the singer arriving at the microphone at intensity $$I_{M}$$ vs. arriving at the listener at intensity $$I_{L}$$, without sound reinforcement. All sound levels are in decibels. By the inverse square law, the relationship between $$I_{L}$$and $$I_{M}$$ is this:
[equation caption=”Equation 4.18″]
$$!I_{L}-I_{M}=20\log_{10}\left ( \frac{D_{s}}{D_{0}} \right )$$
[/equation]
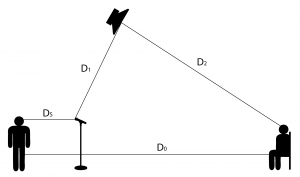
We can also apply the inverse square law to the sound coming from the loudspeaker and arriving at microphone at intensity $$I_{M’}$$ vs. arriving the listener at intensity $$I_{L’}$$, with reinforcement. Feedback occurs where $$I_{M}=I_{M’}$$. Thus we have
[equation caption=”Equation 4.19″]
$$!I_{L’}-I_{M’}=I_{L’}-I_{M}=20\log_{10}\left ( \frac{D_{1}}{D_{2}} \right )$$
[/equation]
Subtracting Equation 4.18 from Equation 4.19, we get
$$!I_{L’}-I_{L}=20\log_{10}\left ( \frac{D_{1}}{D_{2}} \right )-20\log_{10}\left ( \frac{D_{s}}{D_{0}} \right )$$
$$!I_{L’}-I_{L}=20\log_{10}\left ( \frac{\frac{D_{1}}{D_{2}}}{\frac{D_{s}}{D_{0}}} \right )$$
$$!I_{L’}-I_{L}=20\log_{10}\left ( \frac{D_{1}\ast D_{0}}{D_{s}\ast D_{2}} \right )$$
$$I_{L’}-I_{L}$$ represents the PAG, the maximum amount by which the original sound can be boosted without feedback.
$$!PAG=20\log_{10}\left ( \frac{D_{1}\ast D_{0}}{D_{s}\ast D_{2}} \right )$$
This is Equation 4.14 originally discussed in Section 4.2.2.1.