4.2.1.1 Real-World Considerations
We now turn to practical considerations related to the concepts introduced in Section 1. We first return to the concept of decibels.
An important part of working with decibel values is learning to recognize and estimate decibel differences. If a sound isn’t loud enough, how much louder does it need to be? Until you can answer that question in a dB value, you will have a hard time figuring out what to do. It’s also important to understand the kind of dB differences that are audible. The average listener cannot distinguish a difference in sound pressure level that is less than 3 dB. With training, you can learn to recognize differences in sound pressure level of 1 dB, but differences that are less than 1 dB are indistiguishable to even well-trained listeners.
Understanding the limitations to human hearing is very important when working with sound. For example, when investigating changes you can make to your sound equipment to get higher sound pressure levels, you should be aware that unless the change amounts to 3 dB or more, most of your listeners will probably not notice. This concept also applies when processing audio signals. When manipulating the frequency response of an audio signal using an equalizer, unless you’re making a difference of 3 dB with one of your filters, the change will be imperceptible to most listeners.
Having a reference to use when creating audio material or sound systems is also helpful. For example, there are usually loudness requirements imposed by the television network for television content. If these requirements are not met, there will be level inconsistencies between the various programs on the television station that can be very annoying to the audience. These requirements could be as simple as limiting peak levels to -10 dBFS or as strict as meeting a specified dBFS average across the duration of the show.
You might also be putting together equipment that delivers sound to a live audience in an acoustic space. In that situation you need to know how loud in dBSPL the system needs to perform at the distance of the audience. There is a minimum dBSPL level you need to achieve in order to get the signal above the noise floor of the room, but there is also a maximum dBSPL level you need to stay under in order to avoid damaging people’s hearing or violating laws or policies of the venue. Once you know these requirements, you can begin to evaluate the performance of the equipment to verify that it can meet these requirements.
4.2.1.2 Rules of Thumb
Table 4.2 gives you some rules of thumb for how changes in dB are perceived as changes in loudness. Turn a sound up by 10 dB and it sounds about twice as loud. Turn it up by 3 dB, and you’ll hardly notice any difference.
Similarly, Table 4.5 gives you some rules of thumb regarding power and voltage changes. These rules give you a quick sense of how boosts in power and voltage affect sound levels.
[table caption=”Table 4.5 Rules of thumb for changes in power, voltage, or distance in dB” width=”60%”]
“change in power, voltage, or distance”,approximate change in dB
power $$\ast$$ 2,3 dB increase
power ÷ 2,3 dB decrease
power $$\ast$$ 10,10 dB increase
power ÷ 10,10 dB decrease
voltage $$\ast$$ 2,6 dB increase
voltage ÷ 2,6 dB decrease
voltage $$\ast$$ 10,20 dB increase
voltage ÷ 10,20 dB decrease
distance away from source $$\ast$$ 2,6 dB decrease
[/table]
In the following sections, we’ll give examples of how these rules of thumb come into practice. A mathematical justification of these rules is given in Section 3.
4.2.1.3 Determining Power and Voltage Differences and Desired Changes in Power Levels
Decibels are also commonly used to compare the power levels of loudspeakers and amplifiers. For power, Equation 4.6 applies — $$\Delta Power \: dB = 10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$.
Based on this equation, how much more powerful is an 800 W amplifier than a 200 W amplifier, in decibels?
$$!10\log_{10}\left ( \frac{800\, W}{200\, W} \right )=10\log_{10}4=6\: dB\: increase \: in \:power$$
For voltages, Equation 4.4 is used ($$\Delta Voltage\:dB=20\log_{10}\left ( \frac{V_{1}}{V_{0}} \right )$$). If you increase a voltage level from 100 V to 1000 V, what is the increase in decibels?
$$!20\log_{10}\left ( \frac{100\:V}{10\: V} \right )=20\log_{10}10=20\:dB \: increase\:in\:voltage$$
[aside]
Multiplying power times 2 corresponds to multiplying voltage times $$\sqrt{2}$$ because power is proportional to voltage squared: $$P\propto V^{2}$$
Thus
$$!110\log_{10}\left ( \frac{2\ast P_{0}}{P_{0}} \right )=$$
$$!10\log_{10}\left ( \frac{\sqrt{2} \ast V_{0}}{V_{0}} \right )^{2}=3\:dB\:increase.$$
[/aside]
It’s worth pointing out here that because the definition of decibels-sound-pressure-level was derived from the power decibel definition, then if there’s a 3 dB increase in the power of an amplifier, there is a corresponding 3 dB increase in the sound pressure level it produces. We know that a 3 dB increase in sound pressure level is barely detectable, so the implication is that doubling the power of an amplifier doesn’t increase the loudness of the sounds it produces very much. You have to multiply the power of the amplifier by ten in order to get sounds that are approximately twice asloud.
The fact that doubling the power gives about a 3 dB increase in sound pressure level has implications with regard to how many speakers you ought to use for a given situation. If you double the speakers (assuming identical speakers), you double the power, but you get only a 3 dB increase in sound level. If you quadruple the speakers, you get a 6 dB increase in sound because each time you double, you go up by 3 dB. If you double the speakers again (eight speakers now), you hypothetically get a 9 dB increase, not taking into account other acoustical factors that may affect the sound level.
Often, your real world problem begins with a dB increase you’d like to achieve in your live sound setup. What if you want to increase the level by ΔdB? You can figure out how to do this with the power ratio formula, derived in Equation 4.11.
[equation caption=”Equation 4.11 Derivation of power ratio formula”]
$$!\Delta dB=10\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
$$!\frac{\Delta dB}{10}=\log_{10}\left ( \frac{P_{1}}{P_{0}} \right )$$
Thus
$$!\frac{P_{1}}{P_{0}}=10^{\frac{\Delta dB}{10}}$$
where $$P_{0}$$ is the starting power, $$P_{1}$$ is the new power level, and ΔdB is the desired change in decibels
[/equation]
It may help to recast the equation to clarify that for the problem we’ve described, the desired decibel change and the beginning power level are known, and we wish to compute the new power level needed to get this decibel change.
[equation caption=”Equation 4.12 Power ratio formula”]
$$!P_{1}=P_{0}\ast 10^\frac{\Delta dB}{10}$$
where $$P_{0}$$ is the starting power, $$P_{1}$$ is the new power level, and ΔdB is the desired change in decibels
[/equation]
Applying this formula, what if you start with a 300 W amplifier and want to get one that is 15 dB louder?
$$!P_{1}=300\,W\ast10^{\frac{15}{10}}=9486\,W$$
You can see that it takes quite an increase in wattage to increase the power by 15 dB.
Instead of trying to get more watts, a better strategy would be to choose different loudspeakers that have a higher sensitivity. The sensitivity of a loudspeaker is defined as the sound pressure level that is produced by the loudspeaker with 1 watt of power when measured 1 meter away. Also, because the voltage gain in a power amplifier is fixed, before you go buy a bunch of new loudspeakers, you may also want to make sure that you’re feeding the highest possible voltage signal into the power amplifier. It’s quite possible that the 15 dB increase you’re looking for is hiding somewhere in the signal chain of your sound system due to inefficient gain structure between devices. If you can get 15 dB more voltage into the amplifier by optimizing your gain structure, the power amplifier quite happily amplifies that higher voltage signal assuming you haven’t exceeded the maximum input voltage for the power amplifier. Chapter 8 includes a Max demo on gain structure that may help you with this concept.
4.2.1.4 Converting from One Type of Decibels to Another
A similar problem arises when you have two pieces of sound equipment whose nominal output levels are measured in decibels of different types. For example, you may want to connect two devices where the nominal voltage output of one is given in dBV and the nominal voltage output of the other is given in dBu. You first want to know if the two voltage levels are the same. If they are not, you want to know how much you have to boost the one of lower voltage to match the higher one.
The way to do this is to convert both dBV and dBu back to voltage. You can then compare the two voltage levels in dB. From this you know how much the lower voltage hardware needs to be boosted. Consider an example where one device has an output level of −10 dBv and the other operates at 4 dBu.
Convert −10 dBV to voltage:
$$!-10=20\log_{10}\left ( \frac{v}{1} \right )$$
$$!\frac{-10}{20}=\log_{10}v$$
$$!-0.5=\log_{10}v$$
$$!10^{-0.5}=v\approx 0.316$$
Thus, −10 dBV converts to 0.316 V.
By a similar computation, we get the voltage corresponding to 4 dBu, this time using 0.775 V as the reference value in the denominator.
Convert 4 dBu to voltage:
$$!4=20\log_{10}\left ( \frac{v}{0.775} \right )$$
$$!\frac{4}{20}=\log_{10}\left ( \frac{v}{0.775} \right )$$
$$!0.2=\log_{10}\left ( \frac{v}{0.775} \right )$$
$$!10^{0.2}\ast0.775=v\approx 1.228$$
Thus, 4 dBu converts to 1.228 V.
Now that we have the two voltages, we can compute the decibel difference between them.
Compute the voltage difference between 0.316 V and 1.228 V:
$$!\Delta dB=10\log_{10}\left ( \frac{1.228}{0.316} \right ) \approx 12\: dB$$
From this you see that the lower-voltage device needs to be boosted by 12 dB in order to match the other device.
4.2.1.5 Combining Sound Levels from Multiple Sources
In the last few sections, we’ve been discussing mostly power and voltage decibels. These decibel computations are relevant to our work because power levels and voltages produce sounds. But we can’t hear volts and watts. Ultimately, what we want to know is how loud things sound. Let’s return now to decibels as they measure audible sound levels.
Think about what happens when you add one sound to another in the air or on a wire and want to know how loud the combined sound is in decibels. In this situation, you can’t just add the two decibel levels. For example, if you add an 85 dBSPL lawnmower on top of a 110 dBSPL symphony orchestra, how loud is the sound? It isn’t 85 dBSPL + 110 dBSPL = 195 dBSPL. Instead, we derive the sum of decibels $$d_{1}$$ and $$d_{2}$$ as follows:
Convert $$d_{1}$$ to air pressure:
$$!85=20\log_{10}\left ( \frac{x}{0.00002} \right )$$
$$!x=10^{\frac{85}{20}}\ast \left ( 0.00002 \right )\approx 0.36\: Pa$$
Convert $$d_{2}$$ to air pressure:
$$!110=20\log_{10}\left ( \frac{x}{0.00002} \right )$$
$$!x=10^{\frac{110}{20}}\ast \left ( 0.00002 \right )\approx 6.32\: Pa$$
Sum the air pressure amplitudes and and convert back to dBSPL:
$$!dBSPL=20\log_{10}\left ( \frac{0.36+6.32}{0.00002} \right )$$
$$!dBSPL\approx 110.5\,dB$$
The combined sounds in this case are not perceptibly louder than the louder of the two original sounds being combined!
4.2.1.6 Inverse Square Law
The last row of Table 4.5 is known as the inverse square law, which states that the intensity of sound from a point source is proportional to the inverse of the square of the distance r from the source. Perhaps of more practical use is the related rule of thumb that for every doubling of distance from a sound source, you get a decrease in sound level of 6 dB. We can informally prove the inverse square law by the following argument.
For simplification, imagine a sound as coming from a point source. This sound radiates spherically (equally in all directions) from the source. Sound intensity is defined as sound power passing through a unit area. The fact that intensity is measured per unit area is what is significant here. You can picture the sound spreading out as it moves away from the source. The farther the sound gets away from the source, the more it has “spread out,” and thus its intensity lessens per unit area as the sphere representing the radiating sound gets larger. This is illustrated in Figure 4.18.
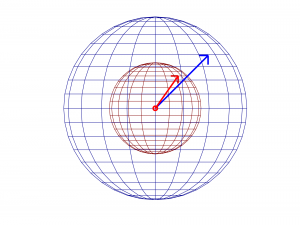
This phenomenon of sound attenuation as sound moves from a source is captured in the inverse square law, illustrated in Figure 4.18:
[equation caption=”Equation 4.13 Inverse square law”]
$$!I_{1}-I_{0}=10\log_{10}\left ( \frac{{r_{0}}^{2}}{{r_{1}}^{2}} \right )=20\log_{10}\left ( \frac{r_{0}}{r_{1}} \right )dB$$
where $$r_{0}$$ is the initial distance from the sound, $$r_{1}$$ is the new distance from the sound, $$I_{0}$$ is the intensity of the sound at the microphone in decibels, and is $$I_{1}$$ the intensity of the sound at the listener in decibels
[/equation]
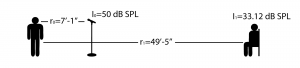
What this means in practical terms is the following. Say you have a sound source, a singer, who is a distance $$r_{0}=$$ 7′ 11″ from the microphone, as shown in Figure 4.19. The microphone detects her voice at a level of $$l_{0}=$$50 dBSPL. The listener is a distance $$r_{1}=$$ 49′ 5″ from the singer. Then the sound reaching the listener from the singer has an intensity of
$$!I_{1}-I_{0}=20\log_{10}\left ( \frac{r_{0}}{r_{1}} \right )$$
$$!I_{1}=I_{0}+20\log_{10}\left ( \frac{r_{0}}{r_{1}} \right )=50+20\log_{10}\left ( \frac{7.0833}{49.4167} \right )=50-16.8728=33.12\, dBSPL$$
Notice that when $$r_{1}<r_{0}$$ the logarithm gives a negative number, which makes sense because the sound is less intense as you move away from the source.
[wpfilebase tag=file id=19 tpl=supplement /]
The inverse square law is a handy rule of thumb. Each time we double the distance from our source, we decrease the sound level by 6 dB. The first doubling of distance is a perceptible but not dramatic decrease in sound level. Another doubling of distance (which would be four times the original distance from the source) yields a 12 dB decrease, which makes the source sound less than half as loud as it did from the initial distance. These numbers are only approximations for ideal free-field conditions. Many other factors intervene in real-world acoustics. But the inverse square law gives a general idea of sound attenuation that is useful in many situations.