In Section 3.1.4 we described the diatonic scales that are commonly used in Western music. These scales are built by making the frequency of each successive note $$\sqrt[12]{2}$$ times the frequency of the previous one. This is just one example of a temperament, a system for selecting the intervals between tones used in musical composition. In particular, it is called equal temperament or equal tempered intonation, and it produces equal tempered scales and intervals. While this is the intonation our ears have gotten accustomed to in Western music, it isn’t the only one, nor even the earliest. In this section we’ll look at an alternative method for constructing scales that dates back to Pythagoras in the sixth century B. C. – just tempered intonation – a tuning in which frequency intervals are chosen based upon their harmonic relationships.
First let’s look more closely and the equal tempered scales as a point of comparison. The diatonic scales described in Section 3.1.4 are called equal tempered because the factor by which the frequencies get larger remains equal across the scale. Table 3.13 shows the frequencies of the notes from C4 to C5, assuming that A4 is 440 Hz. Each successive frequency is $$\sqrt[12]{2}$$ times the frequency of the previous one.
[table caption=”Table 3.13 Frequencies of notes from C4 to C5″ width=”30%”]
Note,Frequency
C4,261.63 Hz
C4# (D4♭),277.18Hz
D4,293.66 Hz
D4# (E4♭),311.13 Hz
E4,329.63 Hz
F4,349.23 Hz
F4# (G4♭),369.99 Hz
G4,392.00 Hz
G4# (A4♭),415.30 Hz
A4,440.00 Hz
A4# (B4♭),466.16 Hz
B4,493.88 Hz
C5,523.25 Hz
[/table]
It’s interesting to note how the ratio of two frequencies in an interval affects our perception of the interval’s consonance or dissonance. Consider the ratios of the frequencies for each interval type, as shown in Table 3.14. Some of these ratios reduce very closely to fractions with small integers in the numerator and denominator. For example, the frequencies of G and C, a perfect fifth, reduce to approximately 3:2; and the frequencies of E and C, a major third, reduce to approximately 5:4. Pairs of frequencies that reduce to fractions such as these are the ones that sound more consonant, as indicated in the last column of the table.
[table caption=”Table 3.14 Ratio of beginning and ending frequencies in intervals” width=”80%”]
Interval,Notes in Interval,Ratio of Frequencies,,Common Perception of Interval
perfect unison,C,261.63/261.63 ,1,consonant
minor second,C C#,277.18/261.63 ,≈ 1.059/1,dissonant
major second,C D,293.66/261.63 ,≈ 1.122/1,dissonant
minor third,C D E♭,311.13/261.63 ,≈ 1.189/1 ≈ 6/5,consonant
major third,C D E,329.63/261.63 ,≈ 1.260/1 ≈ 5/4,consonant
perfect fourth,C D E F,349.23/261.63 ,≈ 1.335/1 ≈ 4/3,strongly consonant
augmented fourth,C D E F#,369.99/261.63 ,≈ 1.414/1,dissonant
perfect fifth,C D E F G,392.00/261.63 ,≈ 1.498/1 ≈ 3/2,strongly consonant
minor sixth,C D E F G A♭,415.30/261.63 ,≈ 1.587/1 ≈ 8/5,consonant
major sixth,C D E F G A,440.00/261.63 ,≈ 1.681/1 ≈ 5/3,consonant
minor seventh,C D E F G A B♭,466.16/261.63 ,≈ 1.781/1,dissonant
major seventh,C D E F G A B ,493.88/261.63 ,≈ 1.887/1,dissonant
perfect octave,C C,523.26/261.63 ,1,consonant
[/table]
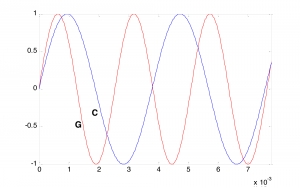
There’s a physical and mathematical explanation for this consonance. The fact that the frequencies of G and C have approximately a 3/2 ratio is visible in a graph of their sine waves. Figure 3.45 shows that three cycles of G fit almost exactly into two cycles of C. The sound waves fit together in an orderly pattern, and the human ear notices this agreement. But notice that we said the waves fit together almost exactly. The ratio of 392/261.63 is actually closer to 1.4983, not exactly 3/2, which is 1.5. Wouldn’t the intervals be even more harmonious if they were built upon the frequency relationships of natural harmonics?
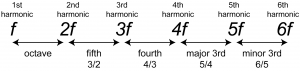
To consider how and why this might make sense, recall the definition of harmonic frequencies from Chapter 2. For a fundamental frequency $$f$$, the harmonic frequencies are $$1f$$, $$2f$$, $$3f$$, $$4f$$, and so forth. These are frequencies whose cycles do fit together exactly. As depicted in Figure 3.46, the ratio of the third to the second harmonic is $$\frac{3f}{2f}=\frac{3}{2}$$. This corresponds very closely, but not precisely, to what we have called a perfect fifth in equal tempered intonation – for example, the relationship between G and C in the key of C, or between D and G in the key of G. Similarly, the ratio of the fifth harmonic to the fourth is $$\frac{5f}{4f}=\frac{5}{4}$$, which corresponds to the interval we have referred to as a major third.
Just tempered intonations use frequencies that have these harmonic relationships. The Pythagoras diatonic scale is built entirely from fifths. The just tempered scale shown in Table 3.15 is a modern variant of Pythagoras’s scale. By comparing columns three and four, you can see how far the equal tempered tones are from the harmonic intervals. An interesting exercise would be to play a note in equal tempered frequency and then in just tempered frequency and see if you can notice the difference.
[table caption=”Table 3.15 Equal tempered vs. just tempered scales” width=”80%”]
Interval,Notes in Interval,Ratio of Frequencies in Equal Temperament,Ratio of Frequencies in Just Temperament
perfect unison,C,261.63/261.63 = 1.000,1/1 = 1.000
minor second,C C#,277.18/261.63 ≈ 1.059,16/15 ≈ 1.067
major second,C D,293.66/261.63 ≈ 1.122,9/8 = 1.125
minor third,C D E_,311.13/261.63 ≈ 1.189,6/5 = 1.200
major third,C D E,329.63/261.63 ≈ 1.260,5/4 ≈ 1.250
perfect fourth,C D E F,349.23/261.63 ≈ 1.335,4/3 ≈ 1.333
augmented fourth,C D E F#,369.99/261.63 ≈ 1.414,7/5 = 1.400
perfect fifth,C D E F G,392.00/261.63 ≈ 1.498,3/2 = 1.500
minor sixth,C D E F G A♭,415.30/261.63 ≈ 1.587,8/5 = 1.600
major sixth,C D E F G A,440.00/261.63 ≈ 1.682,5/3 ≈ 1.667
minor seventh,C D E F G A B♭,466.16/261.63 ≈ 1.782,7/4 = 1.750
major seventh,C D E F G A B ,493.88/261.63 ≈ 1.888,15/8 = 1.875
perfect octave,C C,523.26/261.63 = 2.000,2/1 = 2.000
[/table]