Musicians learn to sing, play instruments, and compose music using a symbolic language of music notation. Before we can approach this symbolic notation, we need to establish a basic vocabulary.
In the vocabulary of music, a sound with a single fundamental frequency is called a tone. The fundamental frequency of a tone is the frequency that gives the tone its essential pitch. The piccolo plays tones with higher fundamental frequencies than the frequencies of a flute, and thus it is higher pitched.
A tone that has an onset and a duration is called a note. The onset of the note is the moment when it begins. The duration is the length of time that the note remains audible. Notes can be represented symbolically in musical notation, as we’ll see in the next section. We will also use the word “note” interchangeably with “key” when referring to a key on a keyboard and the sound it makes when struck.
As described in Chapter 2, tones created by musical instruments, including the human voice, are not single-frequency. These tones have overtones at frequencies higher than the fundamental. The overtones create a timbre, which distinguishes the quality of the tone of one instrument or singer from another. Overtones add a special quality to the sound, but they don’t change our overall perception of the pitch. When the frequency of an overtone is an integer multiple of the fundamental frequency, it is a harmonic overtone. Stated mathematically for frequencies $$f_{1}$$ and $$f_{2}$$, if $$f_{2}=nf_{1}$$ and n is a positive integer, then $$f_{2}$$ is a harmonic frequency relative to fundamental frequency $$f_{1}$$. Notice that every frequency is a harmonic frequency relative to itself. It is called the first harmonic, since $$n=1$$. The second harmonic is the frequency where $$n=2$$. For example, the second harmonic of 440 Hz is 880 Hz; the third harmonic of 440 Hz is 3*440 Hz = 1320 Hz; the fourth harmonic of 440 Hz is 4*440 Hz = 1760 Hz; and so forth. Musical instruments like pianos and violins have harmonic overtones. Drums beats and other non-pitched sounds have overtones that are not harmonic.
Another special relationship among frequencies is the octave. For frequencies $$f_{1}$$ and $$f_{2}$$, if $$f_{2}=2^{n}f_{1}$$ where n is a positive integer, then $$f_{1}$$ and $$f_{2}$$ “sound the same,” except that $$f_{2}$$ is higher pitched than $$f_{1}$$. Frequencies $$f_{1}$$ and $$f_{2}$$ and are separated by n octaves. Another way to describe the octave relationship is to say that each time a frequency is moved up an octave, it is multiplied by 2. A frequency of 880 Hz is one octave above 440 Hz; 1760 Hz is two octaves above 440 Hz; 3520 Hz is three octaves above 440 Hz; and so forth. Two notes separated by one or more octaves are considered equivalent in that one can replace the other in a musical composition without disturbing the harmony of the composition.
In Western music, an octave is separated into 12 frequencies corresponding to notes on a piano keyboard, named as shown in Figure 3.1. From C to B we have 12 notes, and then the next octave starts with another C, after which the sequence of letters repeats. An octave can start on any letter, as long as it ends on the same letter. (The sequence of notes is called an octave because there are eight notes in a diatonic scale, as is explained below.) The white keys are labeled with the letters. Each of the black keys can be called by one of two names. If it is named relative to the white key to its left, a sharp symbol is added to the name, denoted C#, for example. If it is named relative to the white key to its right, a flat symbol is added to the name, denoted D♭, for example.

Each note on a piano keyboard corresponds to a physical key that can be played. There are 88 keys on a standard piano keyboard. MIDI keyboards are usually smaller. Since the notes from A through G are repeated on the keyboard, they are sometimes named by the number of the octave that they’re in, as shown in Figure 3.2.

Middle C on a standard piano has a frequency of approximately 262 Hz. On a piano with 88 keys, middle C is the fourth C, so it is called C4. On the smaller MIDI keyboard shown above, it is C3. Middle C is the central position for playing the piano, with regard to where the right and left hands of the pianist are placed. The standard reference point for tuning a piano is the A above middle C, which has a frequency of 440 Hz. This means that the next A going up the keys to the right has a frequency of 880 Hz. A note of 880 Hz is one octave away from 440 Hz, and both are called A on a piano keyboard.
The interval between two consecutive keys (also called notes) on a keyboard, whether the keys are black or white, is called a semitone. A semitone is the smallest frequency distance between any two notes. Neighboring notes on a piano keyboard (and equivalently, two neighboring notes on a chromatic scale) are separated by a frequency factor of approximately 1.05946. This relationship is described more precisely in the equation below.
[equation caption=”Equation 3.1″]
Let f be the frequency of a note k. Then the note one octave above f has a frequency of $$2f$$. Given this octave relationship and the fact that there are 12 notes in an octave, the frequency of the note after k on a chromatic scale is $$\sqrt[12]{2}\, f\approx 1.05946\, f$$.
[/equation]
Thus, the factor 1.05946 defines a semitone. If two notes are divided by a semitone, then the frequency of the second is 1.05946 times the frequency of the first. The other frequencies between semitones are not used in Western music (except in pitch bending).
Two semitones constitute a whole tone, as illustrated in Figure 3.3. Semitones and whole tones can also be called half steps and whole steps (or just steps), respectively. They are illustrated in Figure 3.3.
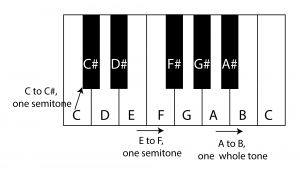
The symbol #, called a sharp, denotes that a note is to be raised by a semitone. When you look at the keyboard in Figure 3.3, you can see that moving up by a semitone takes you to the F key. Thus E# denotes and sounds the same note as F. When two notes have different names but are the same pitch, they said to be enharmonically equivalent.
The symbol♭, called a flat, denotes that a note is to be lowered by a semitone. C♭is enharmonically equivalent to B. A natural symbol ♮removes a sharp or flat from a note when it follows the same note in a measure. Sharps, flats, and naturals are examples of accidentals, symbols that raise or lower a note by a semitone.