Naturally occurring sound waves almost always contain more than one frequency. The frequencies combined into one sound are called the sound’s frequency components. A sound that has multiple frequency components is a complex sound wave. All the frequency components taken together constitute a sound’s frequency spectrum. This is analogous to the way light is composed of a spectrum of colors. The frequency components of a sound are experienced by the listener as multiple pitches combined into one sound.
To understand frequency components of sound and how they might be manipulated, we can begin by synthesizing our own digital sound. Synthesis is a process of combining multiple elements to form something new. In sound synthesis, individual sound waves become one when their amplitude and frequency components interact and combine digitally, electrically, or acoustically. The most fundamental example of sound synthesis is when two sound waves travel through the same air space at the same time. Their amplitudes at each moment in time sum into a composite wave that contains the frequencies of both. Mathematically, this is a simple process of addition.
[wpfilebase tag=file id=29 tpl=supplement /]
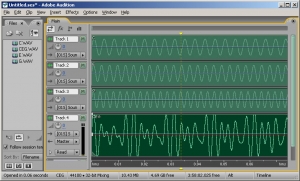
We can experiment with sound synthesis and understand it better by creating three single-frequency sounds using an audio editing program like Audacity or Adobe Audition. Using the “Generate Tone” feature in Audition, we’ve created three separate sound waves – the first at 262 Hz (middle C on a piano keyboard), the second at 330 Hz (the note E), and the third at 393 Hz (the note G). They’re shown in Figure 2.14, each on a separate track. The three waves can be mixed down in the editing software – that is, combined into a single sound wave that has all three frequency components. The mixed down wave is shown on the bottom track.
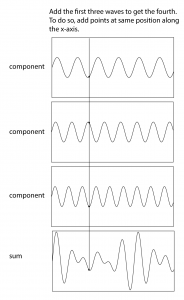
In a digital audio editing program like Audition, a sound wave is stored as a list of numbers, corresponding to the amplitude of the sound at each point in time. Thus, for the three audio tones generated, we have three lists of numbers. The mix-down procedure simply adds the corresponding values of the three waves at each point in time, as shown in Figure 2.15. Keep in mind that negative amplitudes (rarefactions) and positive amplitudes (compressions) can cancel each other out.
We’re able to hear multiple sounds simultaneously in our environment because sound waves can be added. Another interesting consequence of the addition of sound waves results from the fact that waves have phases. Consider two sound waves that have exactly the same frequency and amplitude, but the second wave arrives exactly one half cycle after the first – that is, 180o out-of-phase, as shown in Figure 2.16. This could happen because the second sound wave is coming from a more distant loudspeaker than the first. The different arrival times result in phase-cancellations as the two waves are summed when they reach the listener’s ear. In this case, the amplitudes are exactly opposite each other, so they sum to 0.