2.1.4.1 Resonance as Harmonic Frequencies
Have you ever heard someone use the expression, “That resonates with me”? A more informal version of this might be “That rings my bell.” What they mean by these expressions is that an object or event stirs something essential in their nature. This is a metaphoric use of the concept of resonance.
Resonance is an object’s tendency to vibrate or oscillate at a certain frequency that is basic to its nature. These vibrations can be excited in the presence of a stimulating force – like the ringing of a bell – or even in the presence of a frequency that sets it off – like glass shattering when just the right high-pitched note is sung. Musical instruments have natural resonant frequencies. When they are plucked, blown into, or struck, they vibrate at these resonant frequencies and resist others.
[wpfilebase tag=file id=107 tpl=supplement /]
Resonance results from an object’s shape, material, tension, and other physical properties. An object with resonance – for example, a musical instrument – vibrates at natural resonant frequencies consisting of a fundamental frequency and the related harmonic frequencies, all of which give an instrument its characteristic sound. The fundamental and harmonic frequencies are also referred to as the partials, since together they make up the full sound of the resonating object. The harmonic frequencies beyond the fundamental are called overtones. These terms can be slightly confusing. The fundamental frequency is the first harmonic because this frequency is one times itself. The frequency that is twice the fundamental is called the second harmonic or, equivalently, the first overtone. The frequency that is three times the fundamental is called the third harmonic or second overtone, and so forth. The number of harmonic frequencies depends upon the properties of the vibrating object.
One simple way to understand the sense in which a frequency might be natural to an object is to picture pushing a child on a swing. If you push a swing when it is at the top of its arc, you’re pushing it at its resonant frequency, and you’ll get the best effect with your push. Imagine trying to push the swing at any other point in the arc. You would simply be fighting against the natural flow. Another way to illustrate resonance is by means of a simple transverse wave, as we’ll show in the next section.
2.1.4.2 Resonance of a Transverse Wave
[wpfilebase tag=file id=130 tpl=supplement /]
We can observe resonance in the example of a simple transverse wave that results from sending an impulse along a rope that is fixed at both ends. Imagine that you’re jerking the rope upward to create an impulse. The widest upward bump you could create in the rope would be the entire length of the rope. Since a wave consists of an upward movement followed by a downward movement, this impulse would represent half the total wavelength of the wave you’re transmitting. The full wavelength, twice the length of the rope, is conceptualized in Figure 2.9. This is the fundamental wavelength of the fixed-end transverse wave. The fundamental wavelength (along with the speed at which the wave is propagated down the rope) defines the fundamental frequency at which the shaken rope resonates.
[equation caption=”Equation 2.4″]If L is the length of a rope fixed at both ends, then λ is the fundamental wavelength of the rope, given by
$$!\lambda =2L$$
[/equation]

Now imagine that you and a friend are holding a rope between you and shaking it up and down. It’s possible to get the rope into a state of vibration where there are stationary points and other points between them where the rope vibrates up and down, as shown in Figure 2.10. This is called a standing wave. In order to get the rope into this state, you have to shake the rope at a resonant frequency. A rope can vibrate at more than one resonant frequency, each one giving rise to a specific mode – i.e., a pattern or shape of vibration. At its fundamental frequency, the whole rope is vibrating up and down (mode 1). Shaking at twice that rate excites the next resonant frequency of the rope, where one half of the rope is vibrating up while the other is vibrating down (mode 2). This is the second harmonic (first overtone) of the vibrating rope. In the third harmonic, the “up and down” vibrating areas constitute one third of the rope’s length each.
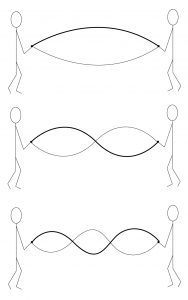
This phenomenon of a standing wave and resonant frequencies also manifests itself in a musical instrument. Suppose that instead of a rope, we have a guitar string fixed at both ends. Unlike the rope that is shaken at different rates of speed, guitar strings are plucked. This pluck, like an impulse, excites multiple resonant frequencies of the string at the same time, including the fundamental and any harmonics. The fundamental frequency of the guitar string results from the length of the string, the tension with which it is held between two fixed points, and the physical material of the string.
The harmonic modes of a string are depicted in Figure 2.11. The top picture in the figure illustrates the string vibrating according to its fundamental frequency. The wavelength l of the fundamental frequency is two times the length of the string L.
The second picture from the top in Figure 2.11 shows the second harmonic frequency of the string. Here, the wavelength is equal to the length of the string, and the corresponding frequency is twice the frequency of the fundamental. In the third harmonic frequency, the wavelength is 2/3 times the length of the string, and the corresponding frequency is three times the frequency of the fundamental. In the fourth harmonic frequency, the wavelength is 1/2 times the length of the string, and the corresponding frequency is four times the frequency of the fundamental. More harmonic frequencies could exist beyond this depending on the type of string.
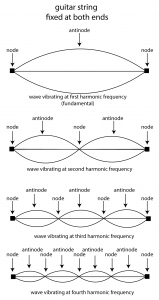
Like a rope held at both ends, a guitar string fixed at both ends creates a standing wave as it vibrates according to its resonant frequencies. In a standing wave, there exist points in the wave that don’t move. These are called the nodes, as pictured in Figure 2.11. The antinodes are the high and low points between which the string vibrates. This is hard to illustrate in a still image, but you should imagine the wave as if it’s anchored at the nodes and swinging back and forth between the nodes with high and low points at the antinodes.
It’s important to note that this figure illustrates the physical movement of the string, not a graph of a sine wave representing the string’s sound. The string’s vibration is in the form of a transverse wave, where the string moves up and down while the tensile energy of the string propagates perpendicular to the vibration. Sound is a longitudinal wave.
The speed of the wave’s propagation through the string is a function of the tension force on the string, the mass of the string, and the string’s length. If you have two strings of the same length and mass and one is stretched more tightly than another, it will have a higher wave propagation speed and thus a higher frequency. The frequency arises from the properties of the string, including its fundamental wavelength, 2L, and the extent to which it is stretched.
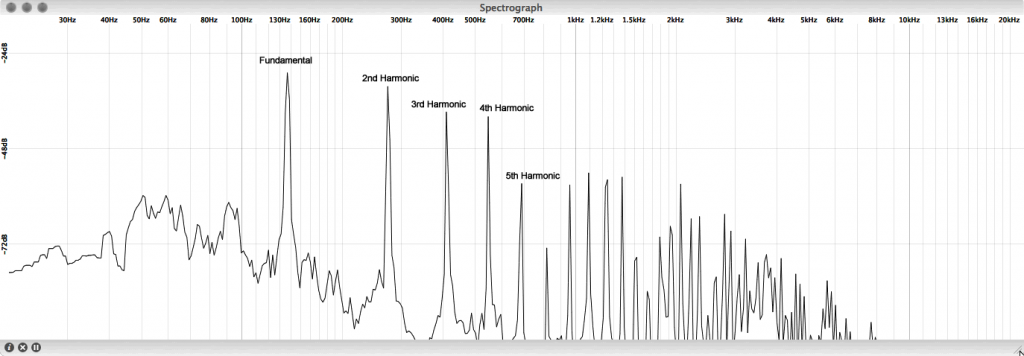
What is most significant is that you can hear the string as it vibrates at its resonant frequencies. These vibrations are transmitted to a resonant chamber, like a box, which in turn excites the neighboring air molecules. The excitation is propagated through the air as a transfer of energy in a longitudinal sound wave. The frequencies at which the string vibrates are translated into air pressure changes occurring with the same frequencies, and this creates the sound of the instrument. Figure 2.12 shows an example harmonic spectrum of a plucked guitar string. You can clearly see the resonant frequencies of the string, starting with the fundamental and increasing in integer multiples (twice the fundamental, three times the fundamental, etc.). It is interesting to note that not all the harmonics resonate with the same energy. Typically, the magnitude of the harmonics decreases as the frequency increases, where the fundamental is the most dominant. Also keep in mind that the harmonic spectrum and strength of the individual harmonics can vary somewhat depending on how the resonator is excited. How hard a string is plucked, or whether it is bowed or struck with a wooden stick or soft mallet, can have an effect on the way the object resonates and sounds.
2.1.4.3 Resonance of a Longitudinal Wave
[wpfilebase tag=file id=131 tpl=supplement /]
Not all musical instruments are made from strings. Many are constructed from cylindrical spaces of various types, like those found in clarinets, trombones, and trumpets. Let’s think of these cylindrical spaces in the abstract as a pipe.
A significant difference between the type of wave created from blowing air into a pipe and a wave created by plucking a string is that the wave in the pipe is longitudinal while the wave on the string is transverse. When air is blown into the end of a pipe, air pressure changes are propagated through the pipe to the opposite end. The direction in which the air molecules vibrate is parallel to the direction in which the wave propagates.
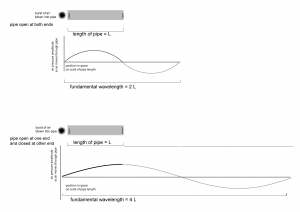
Consider first a pipe that is open at both ends. Imagine that a sudden pulse of air is sent through one of the open ends of the pipe. The air is at atmospheric pressure at both open ends of the pipe. As the air is blown into the end, the air pressure rises, reaching its maximum at the middle and falling to its minimum again at the other open end. This is shown in the top part of Figure 2.13. The figure shows that the resulting fundamental wavelength of sound produced in the pipe is twice the length of the pipe (similar to the guitar string fixed at both ends).
[wpfilebase tag=file id=13 tpl=supplement /]
The situation is different if the pipe is closed at the end opposite to the one into which it is blown. In this case, air pressure rises to its maximum at the closed end. The bottom part of Figure 2.13 shows that in this situation, the closed end corresponds to the crest of the fundamental wavelength. Thus, the fundamental wavelength is four times the length of the pipe.
Because the wave in the pipe is traveling through air, it is simply a sound wave, and thus we know its speed – approximately 1130 ft/s. With this information, we can calculate the fundamental frequency of both closed and open pipes, given their length.
[equation caption=”Equation 2.5″]Let L be the length of an open pipe, and let c be the speed of sound. Then the fundamental frequency of the pipe is.
$$!\frac{c}{2L}$$
[/equation]
[equation caption=”Equation 2.6″]Let L be the length of a closed pipe, and let c be the speed of sound. Then the fundamental frequency of the pipe is .
$$!\frac{c}{4L}$$
[/equation]
This explanation is intended to shed light on why each instrument has a characteristic sound, called its timbre. The timbre of an instrument is the sound that results from its fundamental frequency and the harmonic frequencies it produces, all of which are integer multiples of the fundamental. All the resonant frequencies of an instrument can be present simultaneously. They make up the frequency components of the sound emitted by the instrument. The components may be excited at a lower energy and fade out at different rates, however. Other frequencies contribute to the sound of an instrument as well, like the squeak of fingers moving across frets, the sound of a bow pulled across a string, or the frequencies produced by the resonant chamber of a guitar’s body. Instruments are also characterized by the way their amplitude changes over time when they are plucked, bowed, or blown into. The changes of amplitude are called the amplitude envelope, as we’ll discuss in a later section.
Resonance is one of the phenomena that gives musical instruments their characteristic sounds. Guitar strings alone do not make a very audible sound when plucked. However, when a guitar string is attached to a large wooden box with a shape and size that is proportional to the wavelengths of the frequencies generated by the string, the box resonates with the sound of the string in a way that makes it audible to a listener several feet away. Drumheads likewise do not make a very audible sound when hit with a stick. Attach the drumhead to a large box with a size and shape proportional to the diameter of the membrane, however, and the box resonates with the sound of that drumhead so it can be heard. Even wind instruments benefit from resonance. The wooden reed of a clarinet vibrating against a mouthpiece makes a fairly steady and quiet sound, but when that mouthpiece is attached to a tube, a frequency will resonate with a wavelength proportional to the length of the tube. Punching some holes in the tube that can be left open or covered in various combinations effectively changes the length of the tube and allows other frequencies to resonate.