We assume that you have some familiarity with sine waves from trigonometry, but even if you don’t, you should be able to understand some basic concepts of this explanation.
A sine wave is a graph of a sine function . In the graph, the x-axis is the horizontal axis, and the y-axis is the vertical axis. A graph or phenomenon that takes the shape of a sine wave – oscillating up and down in a regular, continuous manner – is called a sinusoid.
In order to have the proper terminology to discuss sound waves and the corresponding sine functions, we need to take a little side trip into mathematics. We’ll first give the sine function as it applies to sound, and then we’ll explain the related terminology.
[equation caption=”Equation 2.1″]A single-frequency sound wave with frequency f , maximum amplitude A, and phase θ is represented by the sine function
$$!y=A\sin \left ( 2\pi fx+\theta \right )$$
where x is time and y is the amplitude of the sound wave at time x.[/equation]
[wpfilebase tag=file id=106 tpl=supplement /]
Single-frequency sound waves are sinusoidal waves. Although pure single-frequency sound waves do not occur naturally, they can be created artificially by means of a computer. Naturally occurring sound waves are combinations of frequency components, as we’ll discuss later in this chapter.
The graph of a sound wave is repeated Figure 2.4 with some of its parts labeled. The amplitude of a wave is its y value at some moment in time given by x. If we’re talking about a pure sine wave, then the wave’s amplitude, A, is the highest y value of the wave. We call this highest value the crest of the wave. The lowest value of the wave is called the trough. When we speak of the amplitude of the sine wave related to sound, we’re referring essentially to the change in air pressure caused by the vibrations that created the sound. This air pressure, which changes over time, can be measured in Newtons/meter2 or, more customarily, in decibels (abbreviated dB), a logarithmic unit explained in detail in Chapter 4. Amplitude is related to perceived loudness. The higher the amplitude of a sound wave, the louder it seems to the human ear.
In order to define frequency, we must first define a cycle. A cycle of a sine wave is a section of the wave from some starting position to the first moment at which it returns to that same position after having gone through its maximum and minimum amplitudes. Usually, we choose the starting position to be at some position where the wave crosses the x-axis, or zero crossing, so the cycle would be from that position to the next zero crossing where the wave starts to repeat, as shown in Figure 2.4.
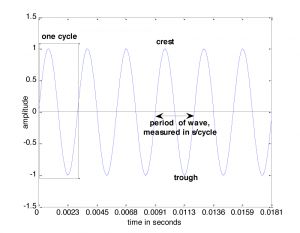
The frequency of a wave, f, is the number of cycles per unit time, customarily the number of cycles per second. A unit that is used in speaking of sound frequency is Hertz, defined as 1 cycle/second, and abbreviated Hz. In Figure 2.4, the time units on the x-axis are seconds. Thus, the frequency of the wave is 6 cycles/0.0181 seconds » 331 Hz. Henceforth, we’ll use the abbreviation s for seconds and ms for milliseconds.
Frequency is related to pitch in human perception. A single-frequency sound is perceived as a single pitch. For example, a sound wave of 440 Hz sounds like the note A on a piano (just above middle C). Humans hear in a frequency range of approximately 20 Hz to 20,000 Hz. The frequency ranges of most musical instruments fall between about 50 Hz and 5000 Hz. The range of frequencies that an individual can hear varies with age and other individual factors.
The period of a wave, T, is the time it takes for the wave to complete one cycle, measured in s/cycle. Frequency and period have an inverse relationship, given below.
[equation caption=”Equation 2.2″]Let the frequency of a sine wave be and f the period of a sine wave be T. Then
$$!f=1/T$$
and
$$!T=1/f$$
[/equation]
The period of the wave in Figure 2.4 is about three milliseconds per cycle. A 440 Hz wave (which has a frequency of 440 cycles/s) has a period of 1 s/440 cycles, which is about 0.00227 s/cycle. There are contexts in which it is more convenient to speak of period only in units of time, and in these contexts the “per cycle” can be omitted as long as units are handled consistently for a particular computation. With this in mind, a 440 Hz wave would simply be said to have a period of 2.27 milliseconds.
[wpfilebase tag=file id=28 tpl=supplement /]
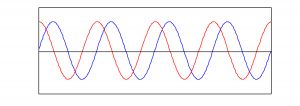
The phase of a wave, θ, is its offset from some specified starting position at x = 0. The sine of 0 is 0, so the blue graph in Figure 2.5 represents a sine function with no phase offset. However, consider a second sine wave with exactly the same frequency and amplitude, but displaced in the positive or negative direction on the x-axis relative to the first, as shown in Figure 2.5. The extent to which two waves have a phase offset relative to each other can be measured in degrees. If one sine wave is offset a full cycle from another, it has a 360 degree offset (denoted 360o); if it is offset a half cycle, is has a 180 o offset; if it is offset a quarter cycle, it has a 90 o offset, and so forth. In Figure 2.5, the red wave has a 90 o offset from the blue. Equivalently, you could say it has a 270 o offset, depending on whether you assume it is offset in the positive or negative x direction.
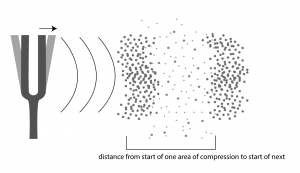
Wavelength, λ, is the distance that a single-frequency wave propagates in space as it completes one cycle. Another way to say this is that wavelength is the distance between a place where the air pressure is at its maximum and a neighboring place where it is at its maximum. Distance is not represented on the graph of a sound wave, so we cannot directly observe the wavelength on such a graph. Instead, we have to consider the relationship between the speed of sound and a particular sound wave’s period. Assume that the speed of sound is 1130 ft/s. If a 440 Hz wave takes 2.27 milliseconds to complete a cycle, then the position of maximum air pressure travels 1 cycle * 0.00227 s/cycle * 1130 ft/s in one wavelength, which is 2.57 ft. This relationship is given more generally in the equation below.
[equation caption=”Equation 2.3″]Let the frequency of a sine wave representing a sound be f, the period be T, the wavelength be λ, and the speed of sound be c. Then
$$!\lambda =cT$$
or equivalently
$$!\lambda =c/f$$
[/equation]
2 comments
Comments are closed.